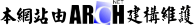國際度量衡SI單位新制與應用(上)
林瑞棋
一、緒言
       國際間以往在度量衡單位使用上，以英制與公制為二大主流，其他依國家之不同，尚有日制、台制、中國標準制與市用制…等之分別，致在國際間形成十分紛繁。
       英制約有一千年的使用歷史，但自十九世紀以後漸漸減少採用，至今僅有美國及少數英國昔日屬地尚在採用。
       公制約有二百的使用歷史，目前尚有七、八十個國家採用。
       國際SI單位新制係於1960年10月國際度量衡局(The International Bureau of Weights and Measures)召開之第11屆度量衡會議中決議，將1866年7月8日所制訂的公制改為「國際SI單位新制(The International System of Units)」，簡稱「SI單位制」，並公佈實施，以求國際間度量衡單位之統一，以方便國際間之交流與更具科學化。
       如今，英國、加拿大、南非、紐西蘭及原採用英制或公制的歐洲國家與世界許多國家亦開始採用，美國與前述已採用SI單位國家交流時，亦不得不被驅策而採用；預料進入公元2000年以後，將是「國際SI單位」普遍化年代。

二、採用SI單位之優點
       採用SI單位優點如下：
       (一)採用SI單位是一貫的，合於邏輯的；各種誘導單位間無換算因子，如一牛頓(newton)的力作用一公尺的能量為一焦耳(joule)，若在一秒鐘所作的功是一瓦特(watt)，毋需作任何換算手續。
       (二)採用SI單位是一絕對制單位的；力與地心引力無關，而依質量之加速度而變化。
       (三)採用SI單位是一致的；不論物理學上的力、熱、電等只有一個單位，如引擎或冷氣機內的功率單位一律用「瓦特(watt)」。
       SI單位的基本單位，長度為公尺(m)，質量為公斤(kg) ，時間為秒(s) ，力為牛頓(N)；依此基本單位導出其他單位如：

面積 平方公尺(m2)
容積 立方公尺(m3)
加速度 公尺每平方秒(m/s2)
力 公斤公尺每平方秒(kg•m/s2)＝牛頓(N)
應力 牛頓平方公尺(N/m2)＝派斯葛(pascal＝pa)

三、SI單位使用時應注意要點
       (一)SI單位中、沒有重量單位，質量在SI單位中用公斤(kg)，力在SI單位中用牛頓(N)；所以在工程結構上的載重或外力，在計算時應加算質量所受的加速度；如一公斤質量在作用於工程結構上的應力為9.807牛頓(N)。
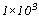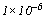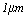       (二)SI單位中採用1000為一進階，在倍數以10的3次方表示；如長度一公尺(m)以公厘(mm)表示時為mm，故在SI單位中沒有公分(cm)單位值，因為公分(cm)為10的2次方，與SI單位10的3次方進階不相符合；如1 000m為1km，又如1 000 000mm為0.000 001m，等於m或以表示。
       (三)通常公制單位中，在四位數以上時，每三位數均以逗點加以區隔，但在SI單位中為避免混亂起見，每三位數則以間隔分開，如公制的35,245,621應寫成為35 245 621；有小數點(decimal point)數值仍以小數點表示外，小數點以下亦以每三位數加以間隔分開，如公制2,015.3216應寫成為
       2 015.321 6。
       (四)使用基本單位二個以上時，則用點加以分開；如工程結構上常用之彎矩(moment)，其單位為牛頓公尺，應寫成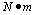，而不能寫成mN，須知mN為表示千分之一牛頓(mollinewton)；又如100m，不能寫成100ms，須知100ms表示千分之一秒(milliseconds)；由於SI單位制對所使用單位均有特別意義，開始使用時必須特別小心。
       (五)對於大數目或小數目之單位，亦可以SI單位記號表示；SI單位對於長度之基本單位為m，其表示方法如(表一)。

表一 SI單位倍數進階數值及長度表示例
SI記號 名 稱 倍 數 例 公尺(m)
G giga       1 000 000 000       Gm＝1 000 000 000＝1×109
M mega       1 000 000       Mm＝1 000 000＝1×106
K kilo       1 000       km＝1 000＝1×103
m milli       0.001       mm＝0.001＝1×10-３
μ micro       0.000 001       um＝0.000 001＝1×10-６
n nano       0.000 000 001       nm＝0.000 000 001＝1×10-９

       由表中顯示在SI單位中大於小數點的數字以10為底的「正指數(positive index)」，小於小數點的數字以10為底的「負指數(negative index)」。
       至於原數值如330 000可以3.3×105表示；原數值0.000 033可以3.3×10-5表示。
       對於分數如3×105×4×103×2×104/5×104×7×106＝3×4×2/5×7×10(12-10) ＝0.686×102或6.86×101或68.6表示。

四、英制、公制單位與SI單位的換算
       在工程應力單位；英制為磅平方吋(psi)，公制為公斤平方公分(kg/cm2)，在SI單位中可以牛頓平方公厘(N/mm2)表示，如以牛頓平方公尺(N/m2)表示，亦稱「派斯葛(pascal)、縮寫為(pa)」；1000牛頓平方公尺，以「KN/m2」表示，縮寫為「Kpa」；1 000 000牛頓平方公尺，以「MN/ m2」表示，縮寫為「Mpa」；其表示如表一中SI記號；如1Mpa換算為英制等於0.145ksi，換算為公制等於1.413t/m2；又如13Mpa，英制等於20Ksi，公制等於97.7 t/m2；(表二)為英制，公制與SI單位之換算示範值。

表二 英制、公制與SI單位換算示範值
英 制 公 制 SI單位
      lin       25.4mm       0.025 400m
      lin2       645.16mm2       6.451 600×104m2
      1ft       304.800mm       0.304 800m
      1lb       0.454kg       4.448 222N
      1kip       0.454tonONT>       4 448.222N＝4.448 222KN
      1psi       0.070kg/cm2＝700kg/m2       6.894 757KN/m2＝0.006 895MN/m2＝0.006 895N/mm2
      1psf       0.488g/cm2＝4.880t/m2       47.880N/m2＝0.047 880KN/m2
      1Ksi       488.0g/cm2＝4.88t/m2       6.894 757MN/m2＝6.894 757Mpa
      1in-lb       1.153kg-cm＝115.3kg-m       0.112 985N•m
      1ft-lb       0.138kg-m       1.355 818N•m
      1in-k       11.53kg-m       112.985N•m
      1ft-k       128.379kg-m       1 355.820KN•m

五、鋼筋混凝土建築物施工模板設計應用
(一)硬木襯板設計
       襯板(sheathing)必須足以承受靜載重(dead load)與施工活載重(live load)的組合載重(combined load)，若每m2承受組合載重kg時，以kg/ m2表示，為換算為SI單位，重量kg必須乘以9.807，因9.807接近10，故得使用10；面積每m2必須除以106，改為N/mm2，則1mm2單位載重wi為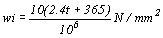式中：
       t＝混凝土版厚度(mm)，2.4＝1m2混凝土版1mm厚度重量(kg)，365＝每m2施工活載重(kg)。
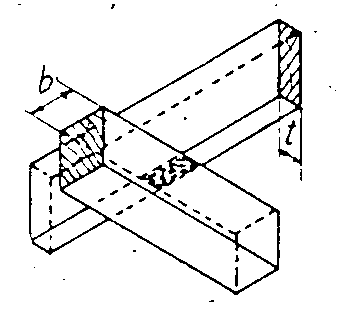
       襯板下由格柵(joist)與縱梁(stringer)支承，並傳遞載重至支柱(shore)，如(圖一)。襯板長度通常跨越數支格柵，故可視為連續梁(continuous beam)，受載後之撓度(deflection)為 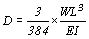式中：
       D＝撓度，W＝載重，L＝跨長，E＝彈性模數，I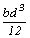＝＝慣性矩，b＝1mm＝時I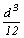＝，W＝wiL。
       依規定連續梁撓度不得大於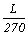，則
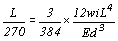
       由前式可導出容許最大跨度為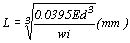
       襯板最小厚度為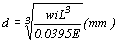

  
  
  
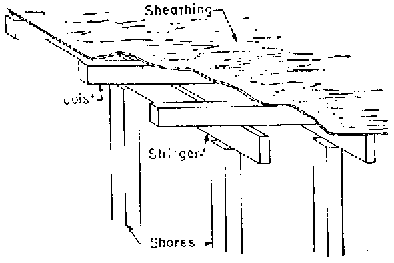附註：
襯板：英國稱decking ，美國稱sheathing
格柵：英、美兩國均稱joist
縱梁：英國稱ledger，美國稱stringer
支柱：英國稱prop，美國稱shore

圖一 混凝土版施工模板構造圖       設計例一
       假設混凝土版厚度＝150mm，襯板厚度＝32mm，彈性模數＝8.3×103N/mm2，則，       單位載重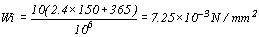
      跨長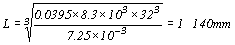
      倘以混凝土版厚度＝150mm，格柵間距＝1 140mm，其襯板厚度為 。
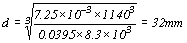(二)夾板襯板設計
       由硬木襯板所述，襯板受載重後之撓度為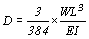與最大容許撓度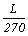，可以導出夾板襯板(plywood decking)最大容許跨長為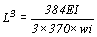或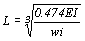
      設計例二        假設混凝土版厚度t＝175mm，夾板厚度d＝19mm，求夾板襯板最大容許跨長L。
       由英國標準CP112 part 2 1971，可查得夾板厚度19mm的慣性矩I＝541mm4/mm，木紋與跨度平行之彈性模數E＝6 210N/mm2，受潮濕條件下時應乘以0.9係數，在暫時載重條件下乘以1.5；因此，在寬度1mm時，I＝541mm4，E＝6 210×0.9×1.5＝8 383N/mm2。
       夾板襯板單位載重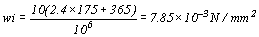
       夾板襯板最大容許長度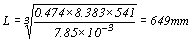
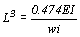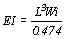       由前述夾板襯板最大容許跨長式中，，其，       設計例三
       假使混凝土版厚度t＝175mm，單位載重wi＝7.85×10-3N/mm2，選用七夾板規格長度為2 400mm，為使夾板襯板頭尾兩端支撐在格柵上，而採用格柵間距L＝480mm，則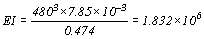
       由標準材料表中可以查到五夾板厚度12.5mm，其I＝155mm4/mm，木紋與跨度平行之E＝8 353N/mm2，則EI＝155×8 353＝1.294×106，EI值明顯不足；改試用夾板厚度15mm之六夾板時，I＝270mm4，E＝8 340N/mm2，在受潮濕及暫時載重條件修正後之E＝8 340×0.9×1.5＝11 259N/mm2，故EI＝11 259×270＝3.04×106，較1.832×106為大，足可採用。
(三)格柵角材設計
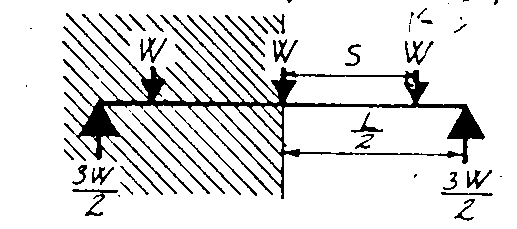
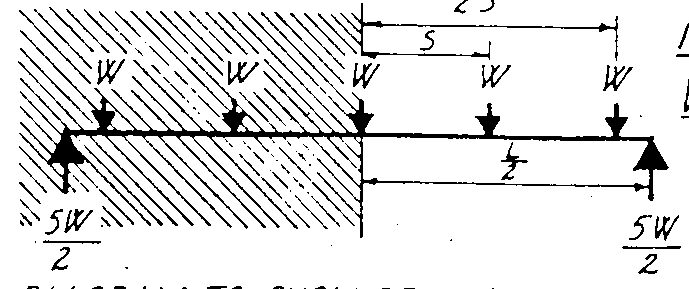
       格柵(joist)所承受的總載重W＝wi(N/mm2)×S(mm)×L(mm)，襯板跨長L在格柵設計時，變成格柵間距S，格柵底面兩縱梁(stringer)間的距離成為格柵的跨長L，應加以說明。
       當格柵承受1mm寬大載重與襯板比較，由於使用彎矩公式，對彎曲前限制撓度影響似有不足；而對wi、S與L值必須併入如W因數在程式，則 或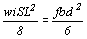
       由於活載重分佈於大面積，其結果將少於集中載重，所以活載重值195kg/m2，已足夠，因此
       單位載重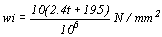
       據此、可以計算(a)格柵角材尺寸，(b)格柵角材跨長，(c)格柵角材間距。
      (a)格柵角尺寸之計算
      設計例四
       假設格柵角材跨長L＝1 800mm，格柵角材間距S＝600mm，混凝土版厚度t＝150mm，格柵角材容計彎曲應力f＝7N/mm2。
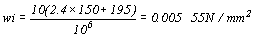，則
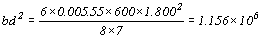
       令b＝50mm，則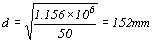
       尚可採用150×50mm格柵角材。
      (b)格柵角材跨長設計

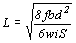
      設計例五        假使格柵彎曲應力f＝7N/mm2，b＝75mm，d＝125mm，格柵角材間距S＝450mm，混凝土版厚度t＝150mm，則
      跨長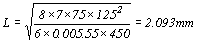
      (c)格柵角材間距設計
      間距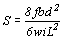

<未完待續>

國際度量衡SI單位新制與應用(下)
林瑞棋

      <接240期>
      設計例六
       假設f＝7N/mm2，b＝50mm，d＝150mm，混凝土版厚度t＝150mm，格柵角材跨長L＝2 000mm，則

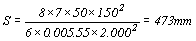
(四)梁底襯板(Beam bottoms)與臨時支柱(shores)設計
       梁底襯板承受1mm寬的載重，可使用與混凝土版木襯板相同載重，寬度b可視同混凝土梁寬度。
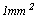之wi值為格柵角材與梁兩側間混凝土版及梁深混凝土靜載重；活載重仍承受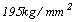；除非梁很深，厚度與跨長將受撓度控制外；通常混凝土梁底襯板厚度為50mm；因此、跨長或支柱(shores)之間距，將受來自梁單位載重控制，而採用木襯板使用跨長公式設計；至於其容許撓度D＝L/270。
      設計例七
       假設混凝土梁深為600mm，梁底襯板厚度為44mm，彈性模數E＝8.3×103N/mm2，從
       跨長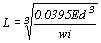
       單位載重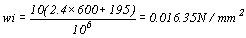
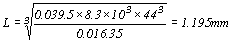
       混凝土梁及其兩側跨長之半的混凝土版與支柱(shores)間距的載重量由臨時支柱承受。
      臨時支柱的載重計算
      設計例八
       假設混凝土版厚度為150mm，臨時支柱間距為1.200mm，跨距長為2.000mm，混凝土梁斷面為600mm深，寬為300mm；則臨時支柱混凝土版重量Ws＝ｗi×1.200×2.000N，活載重用195kg/m2；混凝土版單位載重
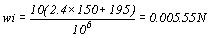
       由臨時支柱所受混凝土版載重Ws＝0.005.55×1.200×2.000＝1.332×104N；混凝土梁的重量Wb＝wi×(臨時支柱間梁的面積＝wi×300×1.200＝5.886N，故臨時支柱所受總載重W＝Ws＋Wb＝13 320＋5 886＝19 206N。
       臨時支柱承受載重確定後，如使用鋼支柱需要斷面尺寸，可自製造廠商提供鋼支柱資料中查得或假設臨時支柱上下兩端為鉸接(hinge)鋼柱，自行設計。
       對使用木材為臨時支柱時，其壓應力必須乘以有效因子(effectire length factor)以決定有效長度，求出容許壓應力，計算容許載重；倘長度超過有效長度時，並可以堅固之水平支撐(rigid horieontal braces)加以聯結，以控制有效長度；依設計規範，木材臨時支柱在乾燥條件下，得提高容許壓應力1.5倍。
       依設計例八，臨時支柱總載重為19 206N，使用40級紅木支柱，在木紋與所受應力平行時，其臨時容許載重為1.65N/mm2，故在有效長度內之最少容許斷面為19 206/1.65＝11 640mm2，倘使用方形角材，其每面寬度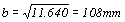，選用市售品規格以125mm×125mm最接近。
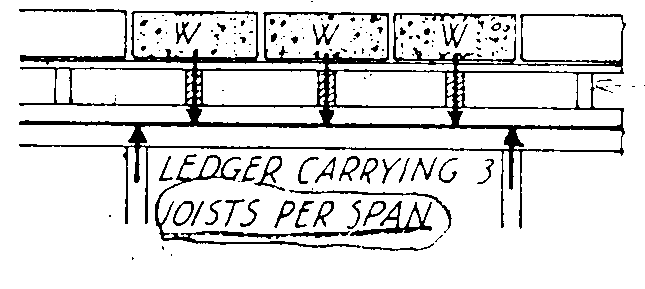
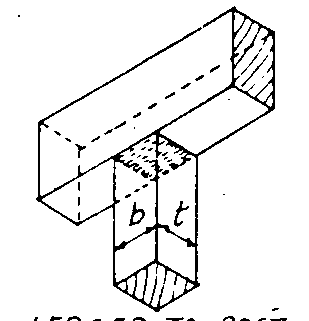
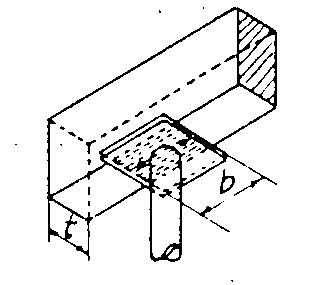
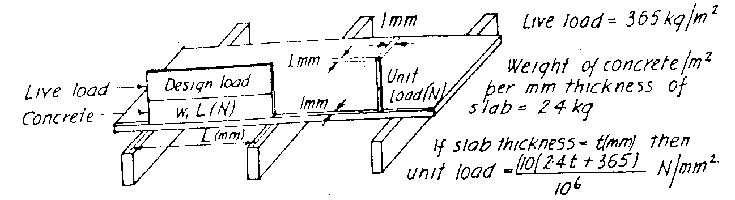
      圖二為版襯板、格柵角材與梁底襯板及支柱之載重綜合說明：

版襯板載重
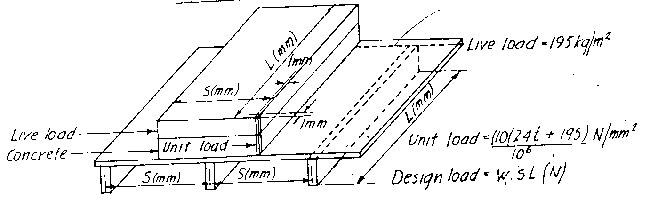
格柵載重
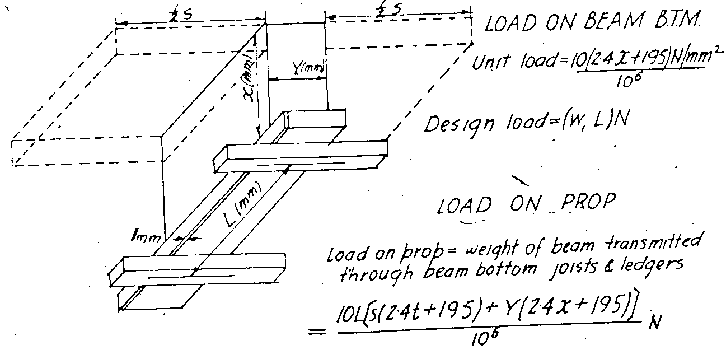
梁底襯板及支柱載重
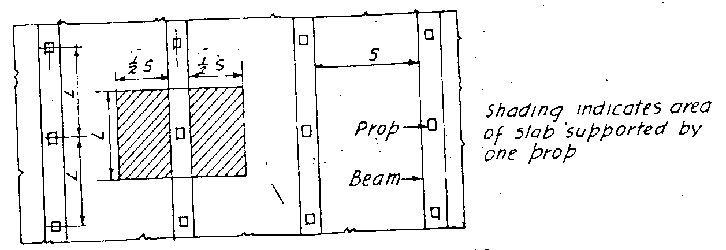版與梁仰視平面圖
圖二 襯板、格柵、梁底襯板及臨時支柱載重

(五)縱梁設計
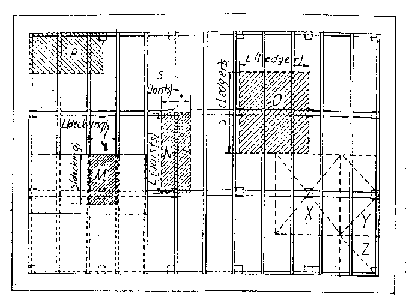
      (a)混凝土版載重面積分佈
      混凝土版的施工載重，由襯板承受後傳遞至襯板下之格柵角材，再由格柵角材傳至格柵下之縱梁(stringer or ledgers)，最後由縱梁傳遞至縱梁下之支柱(shores or props)，各構材載重承受分佈面積如(圖三)混凝土版施工模板系統平面圖所示。

      混凝土版載面積分佈
      M to decking
      N to joist
      0 to ledger of centre
      P to ledger at side
      X to middle prop
      Y to side prop
      Z to corner prop
      P=1/20
      X=0 Y=1/2X
      Z=1/4X
版模平面圖
      
      
      　
版模剖面圖
跨長支承三支格柵角材 彎矩示意圖
      縱梁支承五支格柵
      最大彎矩＝
      
跨長支承五支格柵角材       彎矩示意圖
格柵與縱梁 縱梁與木支柱 縱梁與鋼支柱
邊沿支承面積
圖三 混凝土襯板、格柵、梁底襯板及臨時支柱載重分佈平面與剖面圖

      (b)縱梁承受格柵載重後之最大彎矩
       縱梁(stringers or ledgers)之斷面尺寸與跨長，依格柵傳遞之載重數目，格柵間之間距決定，此處支柱間距亦為縱梁跨長；(圖三)混凝土版模板系統剖面與承受格柵載重數目與格柵間距，如圖表所示。
       當承受三支格柵載重之縱梁最大彎矩(maximum bending moment)為
       當承受五支格柵載重之縱梁最大彎矩為
       式中W＝格柵角材承受載重(N)，L＝縱梁跨長或支柱間距(mm)，S＝格柵角材間距(mm)。
      (c)邊沿支承面積
       如圖三所示，當發生共有方向載重邊沿支承面積時，支柱並不必承受該邊沿支承面積載重；此邊沿支承面積以公厘(mm)計算後乘以1.65N/mm2，即可做為各種情形下的容許總安全壓力。
      (d)連續梁部份跨越支承點的載重
       通常應用於縱梁之設計，是將其視同簡支梁(simply supported bean)以計算出彎矩，然後乘以求出連續縱梁最後彎矩值；對於承受三支格柵的連續縱梁，其彎矩變為
      設計例九
       茲以舉例條件來突顯構材未知斷面尺寸與構材間距之設計，假設混凝土版厚度為200mm，夾板襯板厚度為19mm，格柵角材為150mm×55mm，縱梁間距適合格柵安全跨長，支柱間距為2.4m，則下列各項必須加以計算：
      (1)格柵間距適合襯板。
      (2)縱梁間距適合格柵安全跨長。
      (3)縱梁斷面尺寸足以承受超過2.4m連續跨長的格柵載重。
      (4)支柱斷面假設在垂直間距2m內可以聯結繫桿。
      襯板單位載重
      縱梁與支柱單位載重
      夾板厚度19mm，其木紋與跨長平行，且將受潮濕與臨時載重條件下，其彈性模數E＝8 760×0.9×1.5＝11 825N/mm2，慣性矩I＝577mm4，符合前述條件時，其容許彎曲應力f＝7N/mm2，
      襯板設計最大容許撓度跨長L，則

      假設使用2.4m×1.2m夾板，其最接近格柵間距600mm，無論如何其剩餘部份可利用在樓版終端。
      計算縱梁間距，將使用彎矩求出格柵跨長L，則
      因此，格柵跨長或縱梁斷面尺寸，必須瞭解幾支格柵須在縱梁同一跨長內，當格柵間距為600mm，且一支格柵在縱梁跨長中心，則僅三支格柵角材在縱梁跨架間，故縱梁簡支最大彎矩
      假使縱梁連續跨越三支以上格柵時，其彎矩為 ，因此或
      在縱梁跨長L＝2.4m情形下，無格柵超跨長，則每一支格柵角材所承受的載重W＝wiSL＝0.006 75×600×1 610＝6 038N
      令b＝100mm，則
      故需要縱梁斷面尺寸為2 25mm×100mm
      支柱所承受的載重與格柵的跨長和縱梁的跨長構成的面積關係如圖三所示。
      如在實際上可能發生偏心載重的結果時，為防止不良情形發生，而將設計載重增加3%計算。

六、結語
      國際度量衡SI單位自1960年公佈採行以來，已近四十年，國際間已逐漸普遍採用，惟在台灣國內對工程設計仍沿襲採用舊公制；近年來無論政府或民間雖大聲疾呼加入世界貿易組織(WTO)，但對進入國際交流應具備條件，似未妥善加以規劃準備．一旦進入世界貿易組織，將使已採用SI單位國家無法適應台灣的環境而退縮，台灣想廣泛進行國際交流，因度量衡單位之不同，勢將受到嚴重影響。特以拙文期望政府與民間應加重視世界潮流之趨向，早日預做準備，推行SI單位國際度量衡新制。■