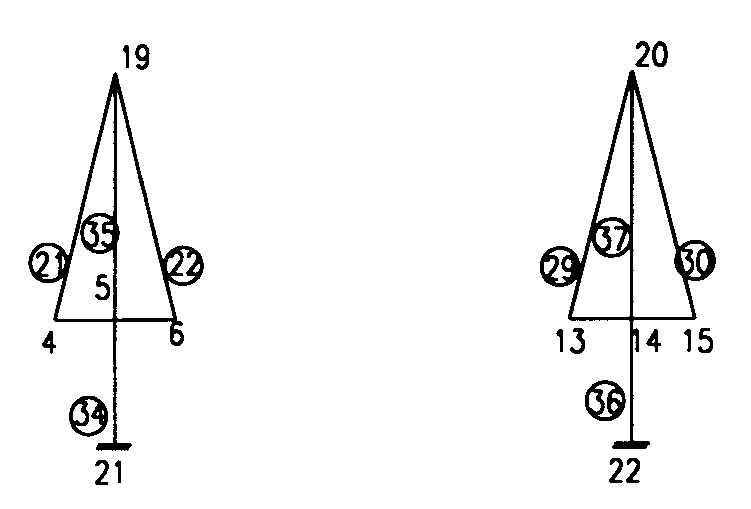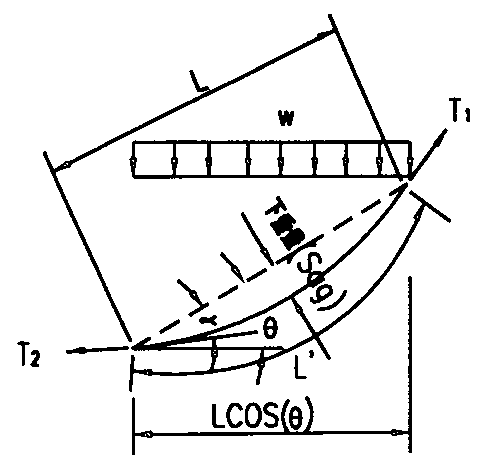
斜張橋或吊橋實際演算之解說
林 楚 儒

關鍵字：斜張橋或吊橋(Cable Stayed or Cable Bridge)

一、前言

         斜張橋或吊橋的分析歷經200年來的演化，已有相當成熟的分析模式，但此皆假設所有構件都不會潛變、乾縮，但事實上，並非如此理想。橋柱或橋台很少為純鋼構，而大部份橋塔採用混凝土的A塔或H塔設計，混凝土的塔柱會有往下縮短的潛變、乾縮行為，而使整座橋的幾何座標改變，甚至使纜繩鬆弛，整體的應力狀態也會有所改變。
         如不考慮混凝土的潛變、乾縮效應，計算斜張橋或吊橋的應力不難，只要利用3D構架程式例如ISDS-STAADIII [1]，或SAP90 [2]等，先給纜繩的初始拉力，試算一次各纜繩的修後E值，輸入程式執行，得出之纜繩之總拉力值，再修正一次新的E值，重新輸入程式執行即可得到滿意之答案。
         但實際結構物並非如此理想，通常橋柱或橋台為鋼筋混凝土結構物，所引起的潛變、乾縮之作用也不容忽視。
         纜繩的應力、應變為非線性變化，但可利用線性程式予以適當的處理甚易得到滿意之結果，如果再考慮混凝土的潛變、乾縮之非線性變化之作用則甚為困難，為了解決此一困境，筆者特地發展TD3F程式以容納鋼及混凝土之非線性行為，以及兩者之間的互制關係以服務工程界。

二、混凝土的非線性反應

         混凝土的潛變、乾縮之非線性行為，請參閱拙著[3]及筆者在本刊上所投稿[4]之文件，詳細情形就不再贅述，因此混凝土之非線性勁度矩陣，須結合纜繩的非線性變化的勁度矩陣一起解。

三、斜張橋或吊橋的理論說明

         斜張或吊橋跟一般的桁架(Truss)的情形不太一樣，是因為重力的關係使纜線產生下垂現象，所以利用纜線來作為結構物，須事先予以施加拉力，使下垂量減少。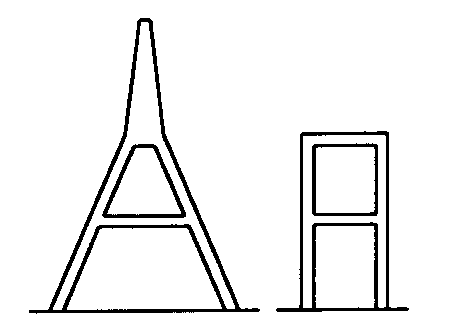

圖一 斜張橋之橋塔型式

         理論上，要使下垂量為零，須施以無限之拉力T，但也因為如此，使纜線的E值降低，如下式所示[5]：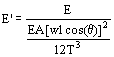
        
         此式子推演如下：
        
         其中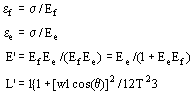為纜線因自重產生下垂而使長度較原先之直線距離稍長量作為應變。
         為纜線因受彈性力所產生之應變。
        
         而
         g為纜線密度，A為纜繩面積。
         s = T/A
         拉力越大，則E’值越接近原E值，理論上拉力T無限大則E’值完全等於原E值。
         水平力H
         先試H=Tcos(q)
        
         H=Tcos(q-a)
         以上連續替代幾次，使算出H值接近上一個H值，則再代入以算出纜線的切線與兩纜線間連線之夾角a。
         下垂量Sag：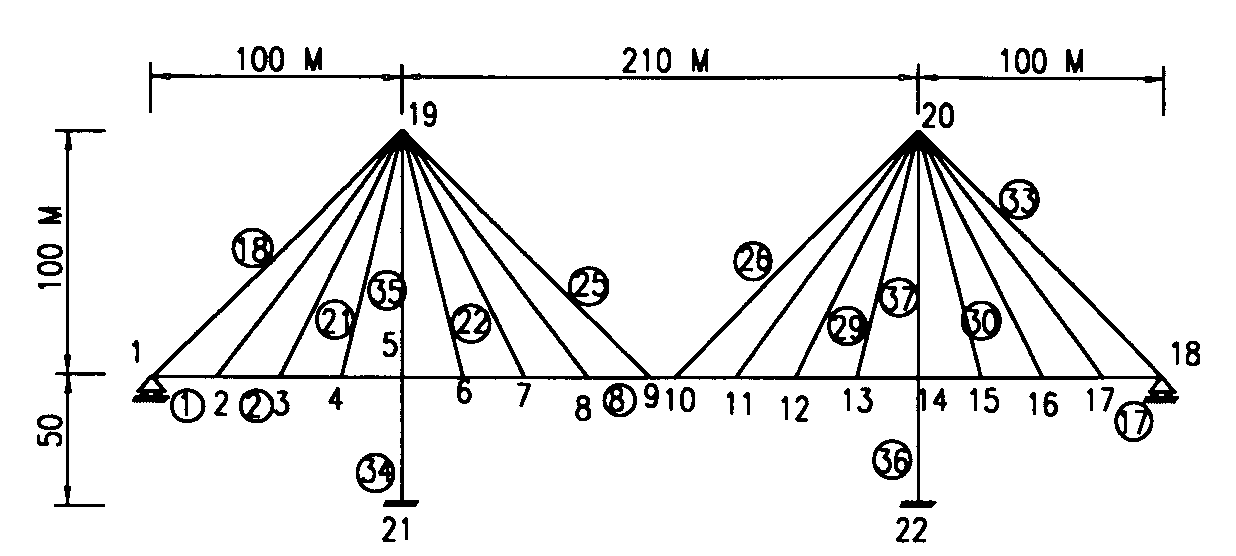
        

圖二 斜張(Cable Stayed)橋

         TD3F程式係利用此非線性理論，重覆計算斜張或吊橋本身受呆重所引起纜線之拉力再修正纜線之勁度矩陣，以符合實際狀況。
         本例題之吊橋的模式建立要非常小心，因纜線之勁度視同內建之三度空間桁架(Space Truss)，下垂之纜線的各結點須予以作外部的MZ束制，如例題之雙箭頭再打叉所示(打叉為束制之意)。

圖三 纜繩受自重影響之情形
圖四 第三施工階段

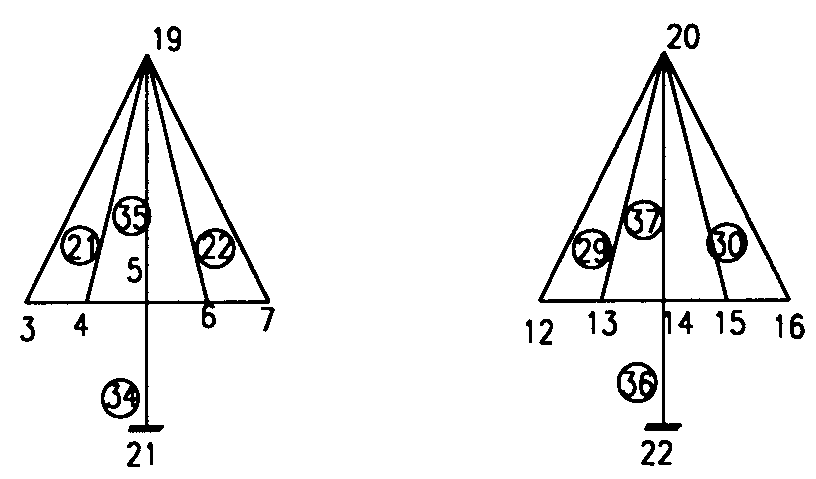
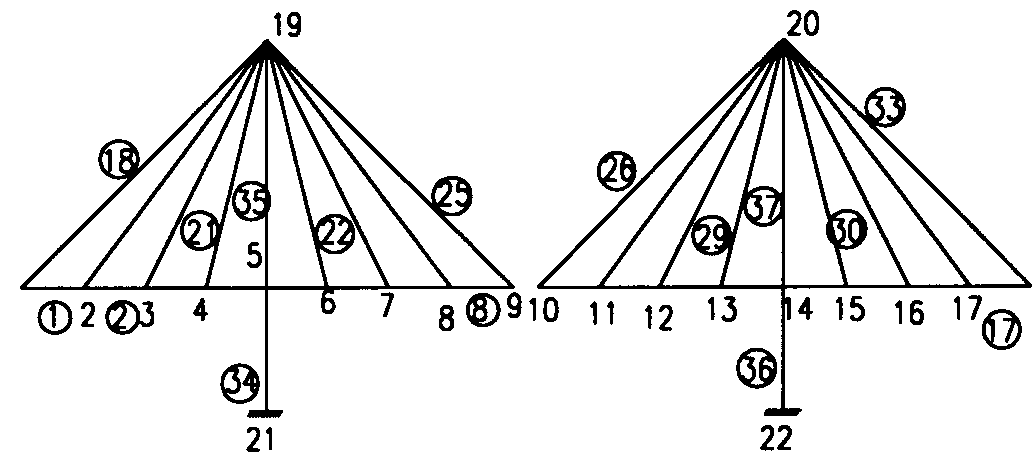
         吊橋的第三施工階段為不穩定結構(中間節塊先吊裝)，須加以人為的彈簧束制，且在第16點加上水平束制(Fx垂直可活動)，到合攏時，這些人工束制通通予以移除，事實上實際施工，也是要將中間節塊用臨時拉桿往兩邊綁到橋柱去，以維持施工中吊橋的穩定。
         斜張橋如果將橋柱擺在橋梁中央，僅能繫拉纜繩於箱型梁中心，此時結構可以二維空間處理，但橋柱若採用雙塔設計則須採用三度空間處理如附圖所示，梁與橋塔連結情形：短棒帶有兩個圓孔表示滑動支承，僅有一個圓孔表示鉸接支承。

圖五 第四施工階段
圖六 第五施工階段

四、斜張橋或吊橋活載重非線性反應之處理

         斜張橋或吊橋之活載重係附加於呆重後之載重，因此纜繩會產生額外之拉力，所以E值尚須修正一次，所幸纜繩活載重所引起之拉力的包絡值(Envelop)，僅有兩個，即零跟最大拉力，因此僅再修正此最大拉力﹝考慮衝擊係數﹞所引起之非線性E值一次即可。

五、纜繩勁度修正之實例演算

         如圖二所示，採用之纜繩E值為1.97×107 T/m2，極限強度12 T/cm2，依表一之方式修正纜繩非線性反應。

表一 應力及E值之非線性反應值
構件 18
33		 19
32		 20
31		 21
30		 22
29		 23
28		 24
27		 25
26		 備註
起始拉力(T) 500 375 250 125 125 250 375 500 起始拉力
為拉緊纜繩勿使其
過份鬆弛。
纜繩面積(cm2) 200 200 100 100 100 100 200 200
E’(107T/ m2) 1.854 1.818 1.940 1.910 1.910 1.940 1.818 1.085
第一次反應力(T) 575.7 891.1 612 433.7 357.7 619.3 976.5 621.1
E’(107T/ m2) 1.892 1.958 1.968 1.969 1.967 1.968 1.960 1.906
第二次反應力(T) 566.0 919 600 435 360 608 1005 606
誤差(%) -1.7 3.1 -1.96 0.3 0.6 -1.8 2.9 -2.4

         由上表可知第三次的修正已沒必要。

六、結論

         斜張橋或吊橋除了解出非線性應力與位移量外，也要同時能解出混凝土的非線性反應之潛變、乾縮等行為，以作為適度的預拱量(Precamber)，或纜繩之日後的鬆弛度之調整。國內最有名的高屏溪斜張橋係單A橋塔的不對稱斜張構造，長斜張這邊為鋼橋，短斜張那邊為預力混凝土橋，使兩邊重量約略相等，而此不對稱斜張反而有孤奇之美，但如果沒有容納混凝土的非線性行為，則此橋根本無法設計，而且結構的分析也要採用3D模式如圖七之立體模式，傳統的二度空間之平面構架梁橋分析心態有必要徹底改變，例如耐震設計就需要第三度的Z向計算。■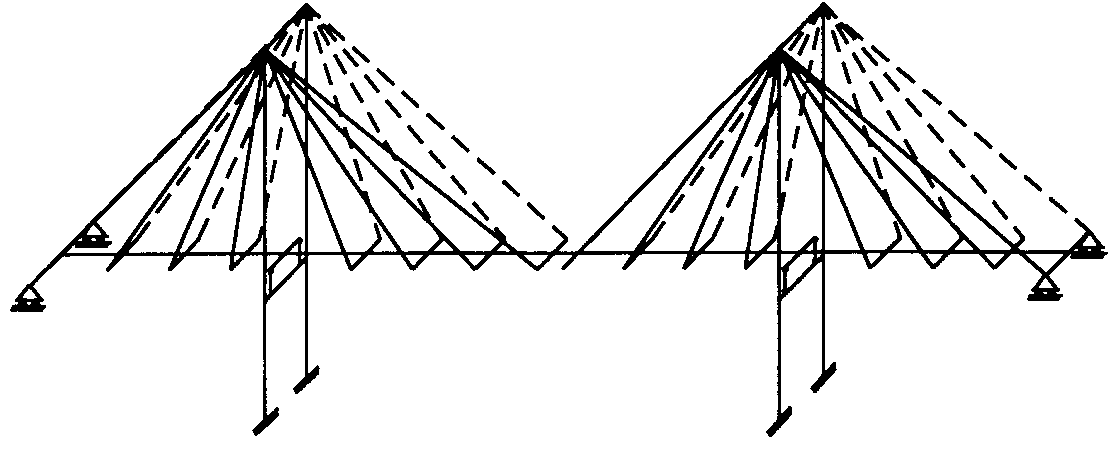

圖七 立體的斜張橋之模型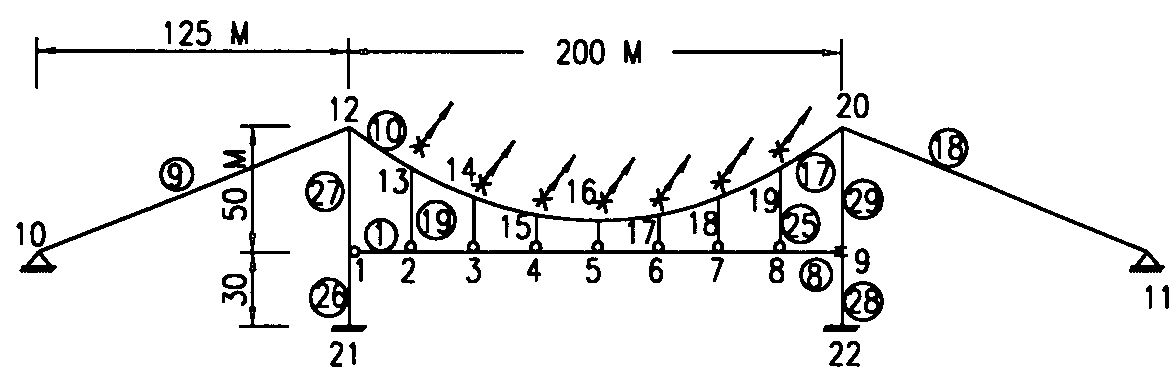

圖八 吊橋(Cable Bribge)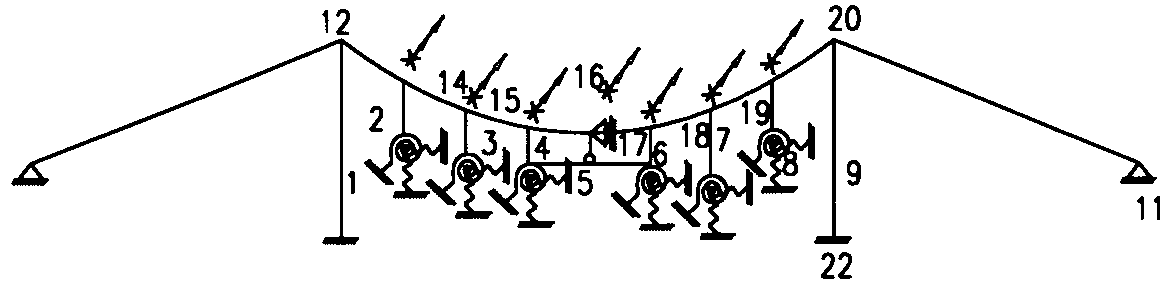

圖九 第三施工階段

參考文獻：

         1.STAAD-III/ISDS, REV. 20, Research Egineers, Inc. 22700 Savi Ranch Pkwy, Yorba Linda, CA 92687, U. S. A.
         2.SAP90 Computer Software for Structural & Earthquake Engineering, Computers and Structures, Inc. 1995 University Avenue, Berkeley, California 94704 U. S. A.
         3.林楚儒-節塊施工的連續預力梁之分析與設計，文笙書局。
         4.林楚儒-齡期係數的重要性及其數值解法現代營建1999, 5月233期。
         5.Ernst H. – J. Der E-Modul von Seilen unter Berucksichtigung des Durchhanges. Bauingenieur, 54, 1979, pp. 321-327。