預力鋼腱連續二次拋物線線形之公式推導

☆ 曾長智 ☆

摘要
         一般傳統預力工字梁或場撐預力箱梁，在橋梁設計考慮預力鋼腱配置時，常採用連續二次拋物線形之設計。不過一般細部設計圖上卻僅標出鋼腱形心各控制點之座標值而已，就設計階段而言此種標示法已能明確指出唯一拋物線形；然施工現場採取每間隔半米或一米就其座標值進行施作及驗收的方式，除控制點外的其他座標值均需由施工單位自行重新計算求得。如果不明瞭連續二次拋物線線形之計算方式，則完成後之預力梁品質堪慮。不諱言，二次拋物線之公式推導屬於國中數學程度，或許就因為太簡單了，所以一般教科書籍中均未予詳述。吾人就多年工地經驗獲知仍有少數監工人員並不明瞭正確線形之重要性及其計算方式。故持擬本文詳細推導拋物線形之基本公式以供參考；並撿選工地最適用之程式型計算機，依其相容語言撰成程式，方便工地監工人員能即時檢核預力鋼腱位置之正確性。

一、基本公式推導

         二次拋物線為一元二次方程式，此種方程式具有三個未知係數，故只須知道三個相關邊界條件即可求解，得一唯一二次拋物線形。從而可求得任一軸向位置之對應高程值。所謂連續二次拋物線係由多段獨立二次拋物線所組合而成。而對任一獨立二次拋物線而言，頭尾銜接其他獨立拋物線處須滿足曲線的連續性(即同一點對應不同段的二次拋物線之高程及斜率須相符)。此點亦成為各段獨立二次拋物線的邊界條件之一。一般連續二次拋物線係由四種基本型式組成，分別解析推導如下：
         (一)左端為最高點，右端為斜率為零之最低點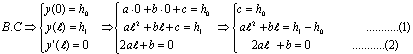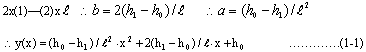



         【解】令此拋物線為y(x)=ax2+bx+c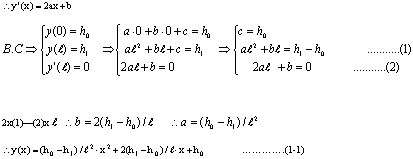

                                           

         (二)左端斜率為零之最低點，右端為最高點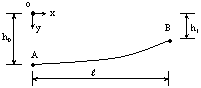


         已知：A點之斜率為零即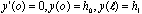
         【解】令此拋物線為y(x)=ax2+bx+c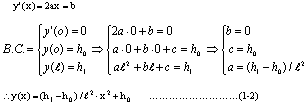

                                           
         (三)左、右端分別為最低高點且斜率為零中間以反曲點銜接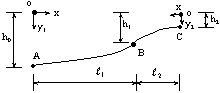

                                           
         已知：1. AB段及AB段分別為拋物線y1及y2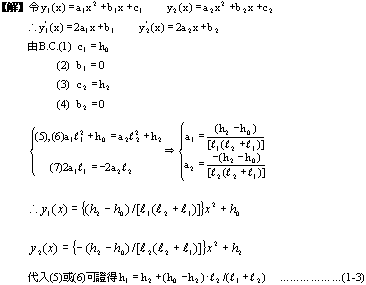
                    
        
                     若將座標系統改如下圖所示：
                     則y1(x1)與前述第(二)項相同直接套用公式(1-2)可得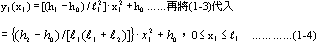
                    
                     而y2(x2)與前述第(一)項目相同直接套用公式(1-1)可得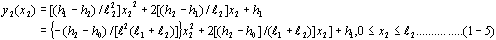
                    
         (四)左、右端分別為最高低點且斜率為零中間以反曲點銜接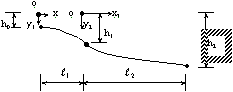

                                           

                 同前述第(三)項之推導方式可得相同結果如下：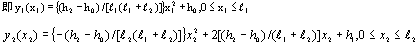
                

二、簡化公式

         由第一項所推得之結論可簡化為下列三種基本公式組合，分別以簡易符號詳列如下以利計算機程式撰寫。
         (一)型式一：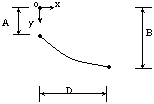

                                           
                 先令K=(B-A)/D2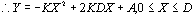
                
         (二)型式二：
        
         (三)型式三：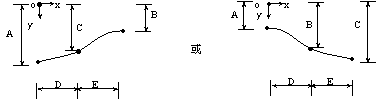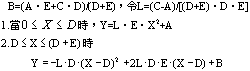
          
        

三、計算機程式撰寫

         吾人採用目前較常用之Casio 880P型程式型計算機撰寫程式，該種語言較接近PC個人電腦常用之培基語言(Basic Language)，具備簡易好學好用之特性。特將程式摘錄如下：
         10 INPUT “SOE(1)；SOS(2)；SOSC(3)Δ=”，N
         20 IFΔN=0 Δ THENΔEND
         30 INPUT “H0=Δ”；A
         40 GOSUB Δ N*100：K=(B-A)/DΛ2：L=(C-A)/((CD+E)*D*E)
         50 INPUT “X=？”，X：IF ΔX          60 ONΔNΔGOTOΔ71，70，72
         70 Y=K*XΛ2+A：GOTOΔ80
         71 Y=-K*XΛ2+2*K*D*X+A：GOTOΔ80
         72 Y=L*E*XΛ2+A：IFΔD          80 PRINT“X=”，X：GOTOΔ50
         100 INPUT“H1=”；B，”Length ΔL=”；D：RETURN
         200 GOSUB Δ100：RETURN
         300 INPUT”H2=”,C,” For．Δ Len．ΔL1=”，D，”Back Δ Len．ΔL2=”E：B=(A*E+C*D)/(D+E)：PRINT”H1=”；B：RETURN

四、結語

         預力梁之細部設計圖由於需求不同，對預力鋼腱配置之表示法亦不盡相同，許多設計單位僅標出一條預力鋼腱的形心線(c•g•s)以代表實際使用的多股預力鋼腱；改由監造單位決定使用多股預力鋼腱之配置方式並詳載於預力梁施工計劃書中。若對二次拋物線形疏忽審查而引致誤差必然嚴重影響預力品質且不符設計圖之需求。故監造單位對二次拋物線預力鋼腱之配置與線形計算需有一定瞭解方能勝任。施工監造能力關乎工程品質甚鉅，如能輔以提昇監造能力則吾輩須盡力而為，亦不可因其過於簡單而忽略之。此篇拋磚引玉之作期能對土木實務作業，有所助益，並激發有志之士共同為土木大業耕耘。■