具重複性施工單元之工程專案排程模擬

☆ 孫國勛 ☆☆ 曾清枝

關鍵字：重覆性單元排程、連續性施工、電腦模擬、學習曲線

摘要
         營建工程雖然是屬於專案型式，但其施工作業規劃中仍可能包含著多個具有重複性施工特性之作業單元，傳統的排程規劃方法如要徑法(CPM)及計劃評核術(PERT)等並未考慮重複性作業之特性，亦未考慮重複性施工單元作業工期之不確定性及學習效應，使得規劃人員於規劃期間無法獲得充足之資訊，影響規劃成果之品質。本研究使用線性工程之特性，並考慮施工單元是否具有學習效應，以電腦模擬方式推估專案之完工時程，結果顯示電腦模擬之結果的確可以提供專案管理者更多之規劃成果資訊。

一、前言

         營建工程一般被歸類為專案型式，亦即其生產型式具有獨特性及唯一性，無法重複性大量生產，傳統的專案排程規劃方法如要徑法(CPM)及計劃評核術(PERT)等 並不考慮重複性作業之特性[1]。然而若詳細探究營建工程之作業流程，則發現其施工作業規劃中仍可能包含著多個具有重複性施工特性之作業單元，例如公路的施築、管線的佈設、橋梁的施工以及高樓的建築等；而且目前之營建工程之設計亦漸漸考慮模組化和標準化，以利大量施工，更使重複性施工單元之排程規劃機會更形增加。由於傳統之專案排程軟體並未設計此一重覆特性，亦未考慮重複性施工單元作業工期之不確定性及學習效應，使得規劃人員於規劃期間無法獲得充足之資訊，影響規劃成果之品質。
         為了改善重複性作業施工排程之效率，學術界陸續提出應用於重複建築單元之線性平衡法(Line-of-Balance，LOB)[3]、使用於高層建築之垂直生產法(Vertical Production Method，VPM) [4]、使用於公路施工之線性排程法(Line Scheduling Method，LSM)[5]、重複排程法(Repetitive Scheduling Method，RSM)[6]等技術的發展，這些方法雖然係針對不同的施工領域所發展，但是都是利用生產曲線的形式來表示個作業項目以及整體工程之進度，如圖一所示，其中生產曲線為直線者表示其生產規劃為連續生產，生產過程不間斷；而生產曲線為折線者表示生產過程需配合其前置作業而有生產間斷時間，形成生產過程有間歇性的現象。
         本研究使用線性工程之特性，並考慮施工單元是否具有學習效應，以電腦模擬方式推估專案之完工時程，並採用先進入先服務(First in first Serves, FIFS)之方式進行專案排程。結果顯示電腦模擬之結果的確可以提供專案管理者更多之規劃成果資訊。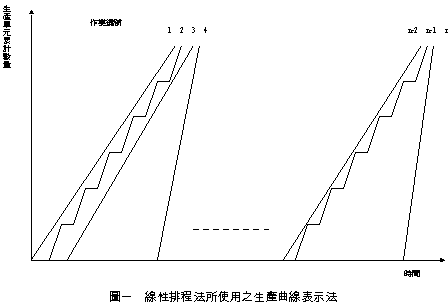

二、重覆施工單元排程之基本原理

         線性工程之施工排程規劃主要為順序性生產的型態，每一個順序性生產過程形成一個作業序列，而每個作業序列之各生產單元又形成一個作業單元的生產序列，為縮短施工期間，通常均會採用重疊施工(Phased or Fast Track Construction)[7]之型態，此時每一個作業單元之前置作業為其順序性生產時作業序列之前置作業以及其前一個作業序列之相同作業項目(單元生產序列)，作業序列與生產單元序列形成交錯的形式，如圖二所示。
         若總共有N個作業序列，每個作業單元以 Ai,j 表示，其中下標 i 表示作業序列之序號而下標 j 表示生產序列之序號，而該作業之耗時(Duration)以 Di 表示。該作業在排程時之預定最早開始時間(Earliest Start Time)以 ESi,j 表示而預定最早完成時間(Earliest Finish Time)以 EFi,j 表示，則在作業單元在儘早施工(As Fast As Possible)的情況下，每個作業單元之預定最早開始時間可以下列公式計算：
ESi,j = Max(EFi-1,j，EFi,j-1)　　於所有的i,j　當 j > 1 　　　　(公式一)
ESi,j = EFi-1,j　　　　　　 　 於所有的i　　當 j = 1　　　　 (公式二)
         而預定最早完成時間可以下列公式計算：
EFi,j = ESi,j + Di 　　　　　　於所有的i,j　　　　　　　 　 (公式三)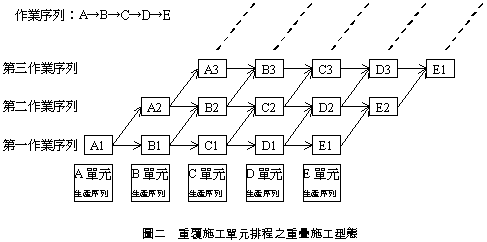


三、學習效應與學習曲線

         自從Wright, T.P. 博士[12]就其觀察經驗發現生產一連串特定機型之飛機時，製造每一架飛機之平均工時會逐次降低之特性而提出學習曲線之觀念後，此一觀點即為各行業所廣泛使用。隨後又有多位學者提出多種學習曲線模式，包括Stanford B模式[13]、立方(cubic)模式[14]、指數(Exponential)模式[15]、片段(Piecewise)模式[16]等
         Wright, T.P. 博士[12]認為當產量增加一倍時，完成最後一各單位所需之生產工時以一固定比率下降，而此一固定比率即稱為學習率r。此一學習曲線模式之函數關係可以表示為：
         f(x)=a1x-b　　　　　　　　　　(公式四)
         其中：
         f(x)：第x單位所需之工時
         a1：生產第一單元所需之工時
         b：學習係數，其與學習率r之關係為：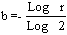
         　　　 　　　　　(公式五)
         此一學習曲線函數(公式四)若兩邊取對數，則可得：
         Log f(x) = Log a1 - b Log x　　　(公式六)
         此一方程式若於雙對數座標繪製時為一線性方程式，因此又稱為對數線性模式(Log-Linear Model)，是目前最為廣泛使用之學習曲線模式。本研究亦採用此一模式作為案例驗證之基礎。

四、具重複性施工單元之工程專案排程模擬

         本文使用前兩節所說明及推導之計算公式，配合應用於Microsoft Excel 2000之@RISK電腦模擬套裝Add-in軟體，進行具重複性施工單元之工程專案排程模擬，並分別考慮以下五種不同之狀況，分別進行電腦模擬分析：
    ●狀況一：不考慮作業時間變異性，不考慮學習效應
    ●狀況二：考慮作業時間變異性，不考慮學習效應
    ●狀況三：不考慮作業時間變異性，考慮學習效應
    ●狀況四：考慮作業時間變異性及平均值學習效應，不考慮標準差學習效應
    ●狀況五：考慮作業時間變異性及平均值與標準差學習效應          其中狀況四及狀況五係模擬兼具變異性及學習效應情況下之專案排程模擬，但此一學習效應應該包括平均作業時間之減少以及標準差範圍之縮小，不過目前本文作者所蒐集之文獻中均未對標準差範圍之縮小提出相關之見解，本文為簡單起見，乃於狀況五中假設標準差範圍之縮小之學習效應之公式計算與學習率數值與平均作業時間相同。

五、案例專案之作業項目基本資料

         本文利用一個假設資訊作為範例進行案例驗證，其作業項目之基本資料如表一所示，每一個作業序列共有A、B、C、D及E等五項作業單元，而生產序列總數共有五個。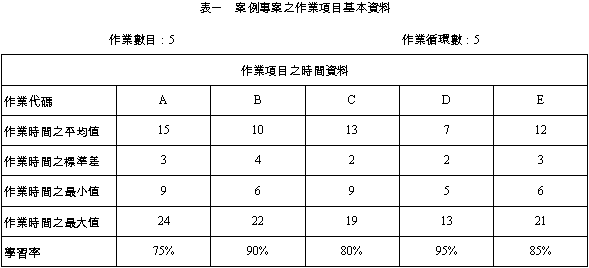


         本研究之作業時間所採用之模擬方式係採用截短式常態分配(Truncated normal distribution)，其作業時間最大值之設定均假設為作業時間平均值加上三倍之標準差，而作業時間最小值之設定則依據工作時間之縮短有一般均較為不易之實際狀況考量而假設為作業時間平均值減去一或二倍之標準差，其中作業A、C、E之作業時間最小值係作業時間平均值減去二倍之標準差，而作業B、D之作業時間最小值係作業時間平均值減去一倍之標準差。
         本研究每一次模擬之計算次數設定為10,000次，取樣方法採用Latin Hypercube形式。
         以下分別就五種設定之狀況加以模擬分析：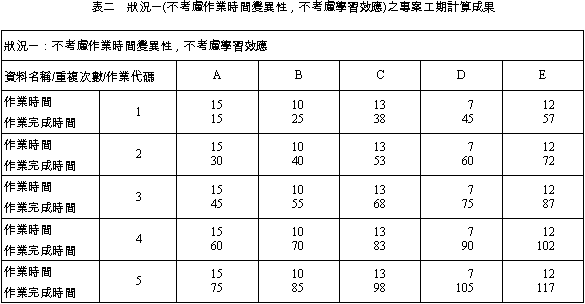
●狀況一(不考慮作業時間變異性，不考慮學習效應)          此時為確定性分析，可直接使用Microsoft Excel之計算功能以公式一、二、三直接計算求解，計算之成果如表二所示。其計算所得之專案完成時間為117天。因為此為確定性計算之成果，因此並不能推知此一專案完成時間之可信度，將使決策者無法預知其所負擔之風險。又因為其並未考慮學習效應所產生之績效提升，將使專案完成時間之預估趨於保守。


●狀況二：考慮作業時間變異性，不考慮學習效應          當考慮作業時間之變異性時，可採用模擬方式求取專案完成時間之平均值與標準差，本狀況模擬所得之專案完成時間之平均值為123.4855天，標準差為6.955375天，最大值為148.6846天，最小值為101.1091天，其分布如圖三所示。
         本狀況模擬所得之專案完成時間平均值較狀況一為高，其原因係因為每一作業之完成時間縮短不易，但若產生延遲則可能有較大之延遲時間，因此專案完成時間將偏高，顯示於狀況一中不考慮作業時間變異性時可能有暴露於較高風險之可能性。而模擬所得之標準差異使決策者對於專案完成時間之可能範圍有較清楚之了解。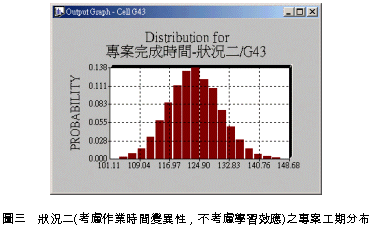
         在圖二之分佈中，亦可發現專案完成時間分佈之最高點位於分佈圖之左側。此乃因為一般作業具有工期縮短較為不易之實際狀況考量而造成，因此模擬後之結果為專案完成時間較長之產生區間較大。
●狀況三：不考慮作業時間變異性，考慮學習效應          此時為確定性分析，可直接使用Microsoft Excel之計算功能以公式一、二、三直接計算求解，作業時間則以公式四及五計算，計算之成果如表三所示。其計算所得之專案完成時間為93.37303天。

         因為此為確定性計算之成果，因此並不能推知此一專案完成時間之可信區間，將使決策者無法預知其所負擔之風險。又因為本狀況增加考慮學習效應所產生之績效提升，使專案完成時間較狀況一縮短了約23.6天。因此若管理者以學習曲線方式分階段訂定合理之績效目標，將可能使專案完成之時間有效率的合理縮短。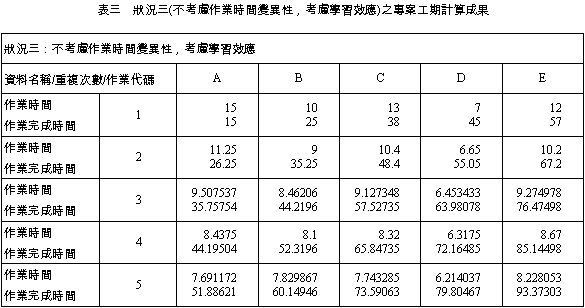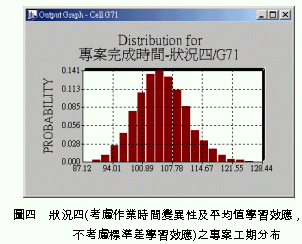


●狀況四：考慮作業時間變異性及平均值學習效應，不考慮標準差學習效應          當考慮作業時間之變異性時，可採用模擬方式求解，又因為考慮作業時間平均值可能因為學習效應而縮短，因此於每一循環時以學習曲線模式(公式四及五)計算原始分佈之作業時間。模擬所得之專案完成時間之平均值為105.233天，標準差為5.900733天，最大值為128.441天，最小值為87.12032天，其分布如圖四所示。
         此一狀況之模擬成果之專案完成時間之平均值較狀況三為大(105.233 - 93.37303 = 11.85997天)，其原因係因為每一作業之完成時間縮短不易，但若產生延遲則可能有較大之延遲時間，因此專案完成時間將偏高，顯示於狀況三中不考慮作業時間變異性時可能有暴露於較高風險之可能性。
         而此一狀況之模擬成果之專案完成時間之平均值較狀況二為小(123.4855 - 105.233 = 18.2525)，亦顯示出學習效應於模擬中亦將發揮其縮短可能完工時間之效果，因此若只考慮單一作業時間而不考慮重複作業之學習效應將可能使工期之估計趨於保守。
●狀況五：考慮作業時間變異性及平均值與標準差學習效應          重複作業之學習效應不只可能使作業時間之平均值降低，亦可能使作業時間的變異性因為逐漸熟練而降低，但一般文獻中對此一效應極少加以研究。本文為模擬此一效應，將原作業時間之標準差以公式四、五之方式加以折減，而其學習率則取為與作業時間之平均值相同。
         當考慮作業時間之變異性時，需採用模擬方式求解，模擬之專案完成時間之平均值為101.0039天，標準差為5.415099天，最大值為125.6225天，最小值為84.37293天，其分布如圖五所示。
         當考慮作業時間的變異性因為逐漸熟練而降低知學習效應時，其模擬所得之作業時間平均值將較狀況四中未考慮時為小(105.233 - 101.0039 = 4.2291天)，此係因為變異數之降低使工期增長之機率降低所造成。而模擬所得之作業時間標準差亦較狀況四中未考慮時為小(5.900733- 5.415099 = 0.485634天)，亦顯示學習效應有降低不確定性之效果。
         綜合以上五種狀況之比較表如表四所示。由@Risk所得之畫面如圖六所示。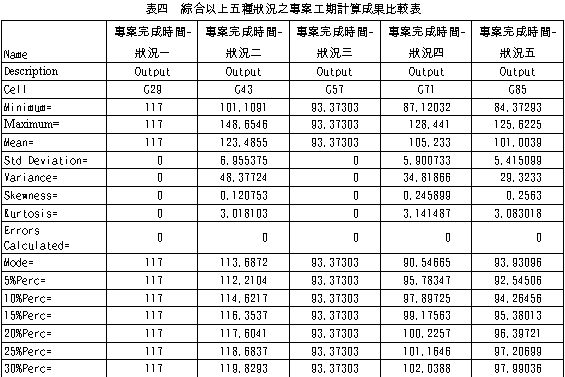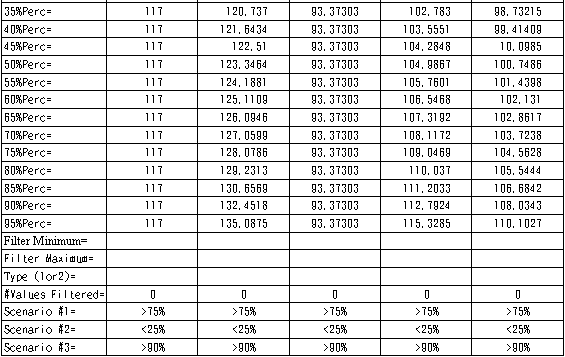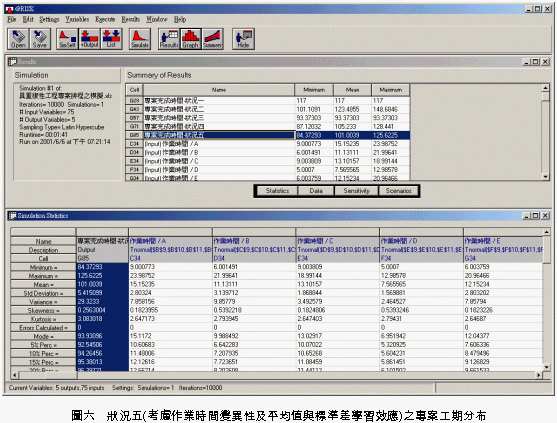






五、結論與建議

         本研究介紹了其結論與建議如下：
(一)營建工程為了提昇施工效率及節省施工成本，目前正極力推動營建自動化，其中施工單元之模組化、標準化及生產方式工業化已成為其中之重要課題，使得重複單元排程技術藝日漸重要，而學習曲線之效應亦將因為施工重複性的增加而日益明顯。
(二)本研究利用線性工程之排程原理進行重覆施工單元排程之模擬，並分別考慮作業時間平均值與標準差之學習效應，並結合目前市面已經普遍使用之商業應用軟體進行模擬分析，可以提供管理者更廣泛之資訊作為決策之參考，立即提昇施工管理之績效。
         後續研究之建議如下：
         1.重複單元排程之問題尚包括資源之有效調配、資源受限條件下對排程之影響、各作業之資源-時間之互換性等，如何達到進度與成本之最佳化，值得更進一步之研究。
         2.本研究僅考慮具有順序性之單線式線性工程，如果為小型網圖形式之重複性工程，應如何簡化其排程工作，值得更進一步之研究。
         3.線性工程之各作業項目於實際執行時，其成本亦有其不確定性，因此並非為一確定值，應可使用機率分布形式或模糊集合方式模擬，這些不確定性對排程規劃有何影響，值得更進一步之研究。■

參考文獻

1.Cole, L. J. R. (1991), “Construction Scheduling: Principles, Practices, and Six Case Studies,” Journal of Construction Engineering and Management, ASCE, 117(4), pp.579-588.
2.Sarraj, Z. M. (1990), “Formal Development of Line-of-Balance Technique”, Journal of Construction Engineering and Management, ASCE, 116(4), pp.689-704.
3.Carr, R. I., and Mayer, W. L. (1974), “Planning Construction of Repetitive Building Units”, Journal of the Construction Division, ASCE, 100(CO3), pp 403-412.
4.James J. O’Brien (1975), ”VPM Scheduling for High-Rise Buildings”, Journal of the Construction Division, ASCE, 101(CO1), pp 895-905.
5.Johnston, D. W. (1981), “Linear Scheduling Method for Highway Construction”, Journal of the Construction Division, ASCE, 107(CO2), pp 247-261.
6.Horris, R. B., and Ioannou, P. G. (1998), “Scheduling Project with Repeating Activities”, Journal of Construction Engineering and Management, ASCE, 124(4), pp.269-278.
7.曾清枝，『專案管理』課程講義，國立中央大學，桃園(2001)。
8.姚乃嘉，『施工規劃與控制』課程講義，國立中央大學，桃園(1999)。
9.黃榮堯，『施工作業規劃與分析』課程講義，國立中央大學，桃園(1999)。
10.邱振崑(2000)，攻心為上-Excel 2000會計、財務管理篇，松崗電腦圖書資料股份有限公司，台灣，台北。
11.Wayne L. Winston(1996), Simulation Modeling Using @RISK, Duxbury Press, Belmont, California.
12.Wright, T. P.(1936), ”Factors affecting the cost of airplanes”, Journal of Aeronautical Sciences, 3(4), pp 122-128.
13.”An improved rationale and mathematical explanation of the progress curve in airframe production”. (1949). Stanford Res. Inst., Stanford, Calif.
14.Carlson, J. G. H. (1973), ”Cubic learning curves: precision tool for labor estimating”, Manufacturing Engrg. And Mgmt., 67(11), pp22-25.
15.”Effect of repetition on building operations and process on site”. (1965). Rep. ST/ECE/HOU/14, United Nations Committee on Housing, Build., and Plng., United Nations, New York, N. Y.
16.Thomas, H. R., Mathews, C. T., and Ward, J. G. (1986), “Learning curve models of construction productivity”, Journal of Construction Engineering and Management, ASCE, 112(2), pp.245-258.