| □倪至寬/台北科技大學 土木與防災研究所 副教授 □李文正/台北科技大學 土木與防災研究所 研究生 □鄭文杰/台北科技大學 工程科技研究所 博士生 |
為了決定光纖感測器於隧道環片的埋設位置,必須了解環片應力分佈的情形。模擬潛盾隧道在軟弱與堅硬黏土、疏鬆與緊密砂土地盤中開挖,分別進行數值分析,評估環片的彎矩、軸力與剪力。考慮光纖感測器的長度,並由分析結果得知,在隧道斷面左右兩側彎曲應力變化較為平緩,同時應力也較大,建議感測器埋設在該處環片內外兩側的鋼筋上,可得到最佳的感測效果。希望未來能進一步將SOFO光纖感測器實際推廣至潛盾隧道環片監測之應用,作為長期的隧道安全監測預警指標。 |
|
一、前言 潛盾隧道以環片為一彈性主體結構,量測環片之內部應變,可實際反應隧道襯砌受周圍之地盤壓力作用下,所產生的應變。若能從混凝土的澆鑄開始至現場環片之裝設過程中,進行變形量測,瞭解混凝土早期變形與裂縫發展等行為,掌握混凝土結構物完整的初始狀態,即可作為回饋設計的珍貴資料。惟環片於製造過程中,須經繁複之蒸汽及水中養生過程,若要將一般傳統感測儀器埋置於環片內,其適用性(例如良率、精度、穩定性、耐久性)相對降低。面對如此難題,應用先進之光纖科技也許可解決部分上述所遭遇的問題,光纖感測器由於本生具有體積小、重量輕、柔軟性高、不受電磁輻射干擾、低傳輸損失、高靈敏度、穩定性高與抵抗環境能力佳等諸多優點,以光纖感測器取代傳統感測器,克服傳統監測系統之不足,於施工或規劃階段,建立具備長期自動化與即時(Real Time)資料擷取功能之安全監測系統,以維護生命財產安全與營運管理績效。 二、研究目的 本研究擬引進瑞士聯邦理工學院所發展出之長範圍光纖感測器-SOFO光纖感測器,嘗試將SOFO光纖感測器預埋置於混凝土梁內,試體的製作過程將模擬實際環片廠的環片製作過程,藉由預埋之SOFO光纖感測器,探討在蒸汽與水中養生過程中混凝土的變形行為,建立材料之初始資料,並驗證SOFO光纖感測器能夠抵抗環片製程時的環境衝擊。在試體製作完成後進行雙點載重試驗,驗證SOFO光纖感測器之適用性。最後為了決定光纖感測器於隧道環片的埋設位置,必須了解環片應力分佈的情形,因此模擬潛盾隧道在軟弱與堅硬黏土、疏鬆與緊密砂土地盤中開挖,分別進行數值分析,了解環片的彎矩與軸力,由不同的受力情形探討SOFO光纖感測器的埋放位置。期望能藉本研究之成果,在未來實際工程上將SOFO光纖感測器應用在潛盾隧道環片,從環片的製程到組裝階段,量測環片內部的初始應變行為,以提供隧道設計作為回饋參考之用。三、光纖感測器 光纖感測器(fiber optic sensor),利用光纖來感測物理量變化的儀器,幾乎可以感測所有傳統感測器所能感測的物理量。將物理量的變化如溫度、應力、轉角、應變、位移、速度、加速度、壓力及磁場等,解調成在光纖內傳輸之光訊號的改變量。除了溫度以外,大部分的物理量改變皆可以由應變的變化經過適當的轉換來獲得。光纖作為結構物的感測元件取代一般傳統的感測器,已經是未來世紀的主要趨勢。(一) 常用於結構物之光纖感測器 1. 麥克生(Michelson)光纖感測器 由兩條單模光纖所組成,一條為參考光纖另ㄧ條為感測光纖,經由參考反射與感測反射形成干涉現象,藉此特性量測作用力與應變,其基本架構如圖一所示。 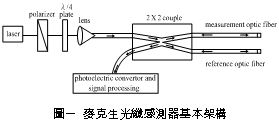 2. 光纖光柵(Fiber Bragg)感測器 將光纖核心之某特定區域,經由紫外光透過一具有週期性明暗分佈的相位光罩(phase mask)照射後,改變該區域核心之折射率,而形成一段具有週期性折射率變化的光纖核心,此區域即稱之為光纖光柵,受到外在因素的影響使得光柵變長或縮短,造成折射率改變,藉此特性量測作用力與應變,其基本架構如圖二所示。 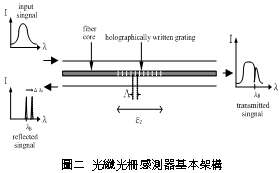 3. 布里淵光時域反射(BOTDR)感測器 於光纖入射端射入一強且窄的光脈衝,造成光纖內晶格振動而產生音波,入射光波與音波相互作用的結果造成光纖折射率的變化,形成散射的現象,每ㄧ條光纖皆具有各自的布里淵散射頻率,當光纖受外力作用時,會使布里淵散射光頻率偏移量產生改變,因此利用頻率偏移變化量的特性量測應變量,其基本架構如圖三所示。 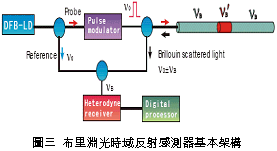 4. 費布里-佩洛干涉式(EFPI)感測器 由單模光纖、多模光纖及一中空矽晶構成,藉由參考反射與感測反射形成干涉現象,造成光強度變化,其基本架構如圖四所示。 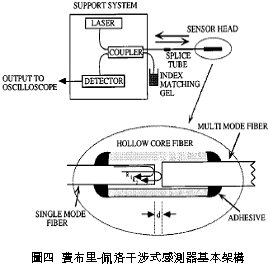 5. 微彎曲(Microbend)光纖感測器 當光纖因外力作用使得光纖曲率發生變化,造成光能量損失,藉此特性量測作用力及應變,其基本架構如圖五所示。 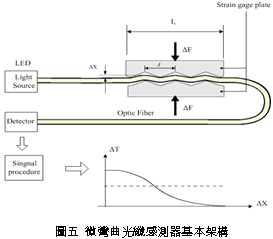 (二) SOFO光纖感測器 SOFO光纖感測系統包括資料擷取單元(reading unit)、光纖感測器、應用軟體及個人電腦等如圖六所示。SOFO感測器在整合性方面有不錯的表現,其已成功地發展出一系列的光纖感測器,如標準型、超長型、薄膜型、高勁度與桁桿型等,以及可用光纖量測溫度、應力的溫度元件(thermocouple)及載重計(load cell)等。此外,透過適當的SOFO轉接器,即能將傳統的感測器整合至同一中央處理系統,更增加了其應用的彈性。 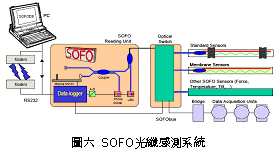 (三) SOFO光纖感測系統特點 優點: 1. 本研究所採用的SOFO光纖感測器,感測範圍為40公分,在40公分內只要任何一點有變形即可量測得到,有別於一般感測器僅針對數公分小範圍的量測。 2. 解析度高,精度為2μm。 3. 耐久性佳,國外超過10年之使用實績,實驗室耐候測試超過30年之穩定性,80%以上良率。 4. 水密性佳。 5. 為全光纖感測器,不受溫度、電磁場、腐蝕、潮濕環境影響。 6. 安裝快速,可裝設在結構物內部或表面。 7. SOFO光纖資料擷取器可與傳統感測器連結並用,亦可透過光纖轉換儀,連結數百群組之感測元件。 缺點: 1. 價格較傳統感測器高出許多。 2. 量測速度需6 ~ 10秒,無法進行動態量測。 3. 無法進行多工性量測。 (四) SOFO光纖系統量測原理 SOFO光纖系統的量測原理為基於雙麥克生干涉儀採串聯形式,其架構如圖七所示,由發光器產生1.3μm紅外線光源,功率0.2mW,經由耦合器將光入射至第一組以麥克生干涉儀系統架構作為感測的光纖,此組光纖內包含一條量測光纖及一條參考光纖,如圖八所示。量測光纖藉由機械式的連結於待測結構物上,使其可隨著結構物而變形,進而量測結構物產生的變化;而參考光纖則不受拘束地安置於光纖管內,不受結構物變形而改變,僅隨著溫度而變,當待測結構物因外在環境因素產生變形,造成不相同路徑而產生相位差,此相位差訊號再經由耦合器連結後送至資料讀取單元,經擷取單元轉換後得到變形量。 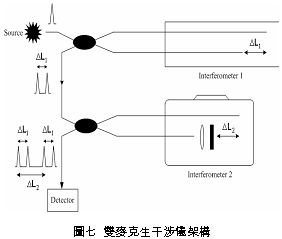 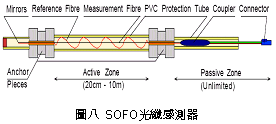 四、試驗規劃 本試驗欲將SOFO光纖感測器預埋於設計的混凝土梁試體內,在試體製作過程中模擬實際潛盾隧道環片的製作過程,包括材料、設計配比、模具、蒸汽養生及水中養生過程等,並於試體製作完成後於實驗室內進行雙點載重試驗,探討光纖感測器是否能在經過繁複的養治條件後,還能夠擁有精確的感測功能。(一) 試體製作 1. 組立試體模具:梁試體尺寸為長116cm、寬25cm、高15cm (如圖九所示)。 2. 鋼筋籠製作:採用6根4號鋼筋,其斷面積為7.6cm2,於試體上下兩面各3根4號鋼筋平均配置,保持斷面的對稱性。 3. 光纖感測器的裝設:於試體製作時將光纖感測器綁扎於上下排中央的主筋上 (如圖十所示)。 4. 溫度計的埋設:為了解於養治過程中試體內部溫度升降的情形,於試體內與光纖感測相同之位置,裝設溫度計。 5. 混凝土拌合。 6. 混凝土坍度量測 (如圖十一所示)。 7. 澆置混凝土 (如圖十二所示)。 8. 蒸汽養生:環片的蒸汽養生作業將會歷經預置期、升溫期、恆溫期、降溫期與冷卻期等五個階段 (如圖十三所示)。 9. 水中養生:將蒸汽養生完成之試體,靜置4小時後拆模,再放入飽和石灰水池中浸泡24小時 (如圖十四所示)。       (二) 雙點載重試驗 於實驗室內驗證光纖感測器量測變形量的精確度,將養治完成的梁試體架設在萬能試驗機台上,進行雙點載重試驗,光纖感測器裝設示意如圖十五所示,量測反覆靜力施載下光纖感測器的變形量,並裝設位移感測器直接測得試體的變位量,如圖十六、圖十七所示。雙點載重施加的方式,造成光纖感測器位置所受到的應力為純彎矩狀態,在此應力作用下光纖感測器每一點的應變量理論上都是相同的,因此曲率為一個常數,藉此特性進一步換算得到變位量,最後將光纖感測器的量測值與位移感測器量測值相互比較驗證其適用性。 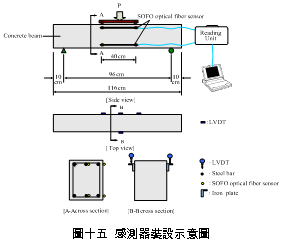   五、試驗結果分析 (一) 試體養治過程監測將光纖感測器埋設於試體內,歷經升溫、恆溫、降溫與冷卻的四個溫度變化的蒸汽養生過程,由圖十八與圖十九皆顯示出當溫度一有變化時,光纖感測器變形量也隨即產生改變 ,由熱脹冷縮的觀點來看,試體溫度上升光纖感測器立即隨著伸長,溫度下降光纖感測器也立即縮短,由此反映出溫度的變化與光纖感測器變形量的變化有非常好的一致性。 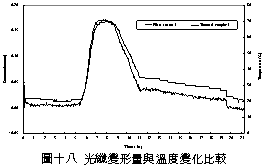 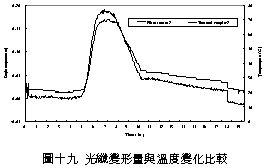 (二) 簡支梁雙點載重結果分析 由試驗結果顯示,即使承受反覆載重條件下,SOFO光纖感測器仍能維持正常的感測功能不致損壞。根據圖二十、圖二十一與圖二十二顯示,比較表面貼附式光纖感測器與內埋式光纖感測器的量測結果,表面貼附式光纖感測器量測結果數值跳動較大,且在每一個載重作用下,所量測到的變形量皆小於內埋式的光纖感測器,可能原因歸納如下: 1. 表面貼附式光纖感測器的裝設方式,是由兩個端點固定在試體表面,由此兩點的變化改變感測器的長度,相較於內埋式的感測器,四周圍都被混凝土包覆著,感測器的變形是隨著試體一起改變,因此不僅僅是在端點的變化,感測段的整個區域都隨著結構物一起變形。 2. 表面貼附式光纖感測器的兩端是採用一種專用的黏著劑以黏貼的方式固定在試體表面,由於黏著劑與試體剛性不同,當試體受力後,並無法將試體真正的變形量傳遞到感測器上。 3. 量測值跳動的情形,是由於表面貼附式光纖感測器的貼附方式,是將感測器兩端點處固定在試體表面,其餘部份皆懸掛在空中,使得有擺動的空間,因此當施加載重時,油壓幫浦會使得整個試體產生微振動,此時感測器無固定處就會隨著振動,造成量測時數據產生跳動的現象。 由光纖感測器量測值推算各載重下梁中點的相對變位,並將推算結果與位移感測計的量測值整理繪製如圖二十三所示,由結果顯示,表面貼附式的光纖感測器的變位值在前幾個小載重階段時,變位值與內埋式感測器和表面貼附式光纖感測器的量測值都非常接近,但當載重持續增大內埋式感測器與理論解之誤差量就跟著增大,而位移感測計的量測值則在整個加載階段不斷飄移,因滾支承(roller)附近梁試體混凝土由於應力集中而破碎,故加載過程中混凝土梁並非平穩置放於載重架(loading frame)上,而有些微傾斜。但整體而言內埋式感測器的量測值與理論解比對結果,得到良好的ㄧ致性,在此驗證了內埋式光纖感測器的適用性與準確性。 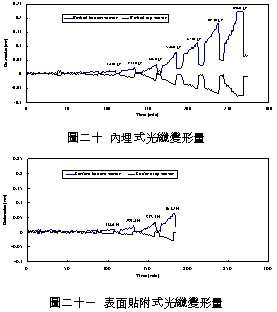 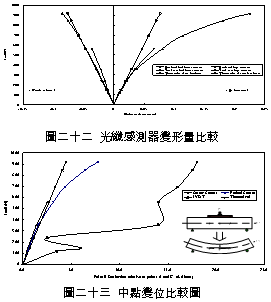 六、數值分析 採用PLAXIS 有限元素分析程式作為數值分析工具。分別針對潛盾隧道在黏土與砂土層兩種不同的覆土情形下,比較軸力與彎矩分佈等情形,並建議於後續應用時感測器所需埋放的位置。(一) 模型建立 1. 分析模式的選擇:分析採用二維的平面應變(plain strain)模式分析。 2. 幾何形狀描繪:按照欲分析之隧道模型,將隧道與周圍土層的幾何形狀作適當的描繪。 3. 邊界條件設定:界定底部水平方向為鉸接(hinge),左右兩側垂直方向為滾支承(roller),土壤變形的模式只允許上下位移而不能左右位移。 4. 界面元素設定:PLAXIS程式以Rinter參數控制界面元素的勁度,若Rinter = 1代表土壤與結構物勁度相同,Rinter<1代表土壤勁度小於結構物勁度,本研究分析時採用Rinter = 0.7。 5. 組合律:假設土壤為均質(homogeneous)、等向(isotropic)及應力應變關係為完全彈性塑性(elasto-perfectly plastic),破壞準則為線性之莫爾庫倫準則。 (二) 模型建立 土壤參數如表一所示,環片參數如表二所示。 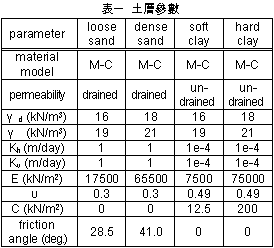  (三) 分析結果 比較砂土地盤與黏土地盤的分析結果如圖二十四與圖二十五所示,其彎矩與軸力分佈趨勢皆相同,但砂土地盤所產生的最大彎曲力矩皆大於黏土地盤許多,而軸力的最大值則相差不大。  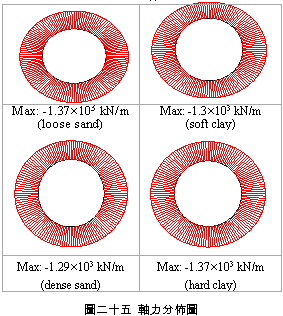 本研究所採用的SOFO光纖感測器長度為40公分,因此量測到的應變量為40公分區域的平均應變量,將感測器埋設在應變分佈較為平均的位置,應該可得到較佳的感測效果。根據數值分析結果顯示,軸力幾乎是平均分佈在環片結構上,而彎矩的分佈則有較大變化,因此將SOFO光纖感測器埋設在彎矩變化較為平緩的位置,將會得到較佳的結果。綜合上述結果,建議SOFO光纖感測器埋置於環片結構的位置如圖二十六所示,將感測器埋置在隧道斷面的左右兩側,可得到最佳的感測效果。 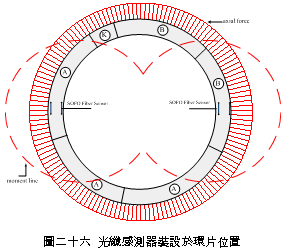 七、結論與建議 (一) 結論1. 本研究將SOFO光纖感測器預先埋設於混凝土梁試體中,試體的製作方式模擬預鑄環片廠的環片製作過程,在整個過程中,光纖感測器歷經了混凝土澆置時的衝擊、振動台的振動、蒸汽養生與水中養生等過程,並在全程中持續進行資料測讀,結果顯示感測器一直維持良好的感測功能。 2. 表面貼附式光纖感測器與內埋式光纖感測器的量測結果,表面貼附式光纖感測器量測結果數值跳動較大,而且在每一個載重作用下,所量測到的變形量皆小於內埋式的光纖感測器,因此將SOFO光纖感測器內埋於結構物中,將會得到較佳的感測效果。 3. 本研究比較內埋式及表面貼附式光纖感測器的量測值與位移感測器的量測值,其中又以內埋式感測器與理論解較為接近,在此又進一步的驗證了,將SOFO光纖感測器內埋於結構物中準確性較佳。 4. 由數值分析結果顯示不論是潛盾隧道於砂土或黏土地盤情形下,皆應該將光纖感測器埋置於隧道斷面的左右兩側,即可得到最佳的感測效果。 (二) 建議 1. 根據本研究實驗的驗證結果顯示,SOFO光纖感測器可完全承受預鑄環片製程時的環境衝擊,在此建議可將SOFO光纖感測器預埋於潛盾隧道的環片中,從混凝土澆鑄開始就對其變形進行量測,瞭解環片早期變形行為,建立環片材料之初始變形資料,並對於環片襯砌嵌入完工後進行長期之監測作業,掌握環片整體的變形行為。 2. 本研究所採用的光纖感測器只有SOFO應變式光纖感測器一種,建議未來可針對其它種類的光纖感測器,如光纖光柵與布理淵光纖感測器等在國內技術較為純熟的光纖感測器,比較不同光纖感測器對於潛盾隧道的適用性。 3. SOFO光纖感測器經過設計可製成各種感測器,如應變計、溫度計、位移計、傾斜計、應力計與水壓感測器等。本研究只有採用應變式感測器,故只能對應變感測器所得結果提出驗證,未來如果工程案例需要,將可利用已開發之光纖感測器量測設計參數,並驗證各項感測器之效能。 4. 要將光纖感測器埋設於潛盾環片內,仍有許多施工上的問題須克服,後續研究建議可針對如何以不影響環片施工的方式,按照預鑄環片廠實際製作之生產流程,提出可行之光纖感測器預埋方法,並規劃配合潛盾際隧道工程進度進行量測作業的方式。■ 參考文獻 1. 吳嘉原,「橋樑監測之感側技術」,國立中央大學土木工程研究所碩士論文,民國91年6月。2. 張連壁,「光纖感測器」,文笙書局,民國87年。 3. 林詠彬、潘治良、郭原宏、林子剛、張國鎮,“光纖感測器於土木工程之應用”,土木水利,第二十九卷,第三期,第69-78頁,民國91年11月。 4. 張國鎮、林詠彬,「光纖感測監測之應用與發展研討會論文集」,國家地震工程研究中心,民國92年11月。 5. 畢衛紅,“高分辨率麥克爾遜光纖應變傳感器”,光學精密工程,第8卷,第1期,第83-86頁,民國91年2月。 6. Timothy A. Hampshire. 2000. Monitoring the behavior of steel structures using distributed optical fiber sensors. Journal of Constructional Steel Research 53: 3,267–3,281. 7. Gunther Wehrle, Percy Nohama1, Hypolito Jose Kalinowski1, Pedro Ignacio Torres and Luiz Carlos Guedes Valente. 2001. A fibre optic Bragg grating strain sensor for monitoring ventilatory movements. Measurement Science and Technology 12: 805–809. 8. Tsuneo Horiguchi, Toshio Kurashima and Mitsuhiro Tateda. 1989. Tensile strain dependence of Brillouin frequency shift in silica optical fibers. IEEE Photonics Technology Letters 1: 5,107–5,108. 9. T. Kurashima, T. Horiguchi, H. Izumita, S. Furukawa and Y. Koyamada. 1993. Brillouin optical-fiber time domain reflectometry. IEICE Trans. Commun. E76–B: 4(2). 10. Jiang M and Gerhard E. 2001. A simple strain sensor using a thin film as a low-finesse fiber-optic Fabry-Perot interferometer. Sensors Actuators A: 88,41–88,46. 11. D. Inaudi, Sandra LLoret. 1997. Ranging of reflective markers in optical fiber sensors by double-pass phase modulation. Optical Engineering 36: 9,2457–9,2465. 12. R.B.J. Brinkgreve. 1998. PLAXIS 2D-Version 7. Rotterdam. Netherlands: A.A. Balkema. 13. Dennis, Derickson. 1998. Fiber optic Test & measurement Prentice Hall, 134. 14. K.T.V. Grattan, B.T. Meggitt. 1999. Optical Fiber Sensor Technology 3. Kluwer Academic Publishers, 225–240. 15. D. Inaudi. 2000. Application of Civil Structural Monitoring in Europe Using Fiber Optic Sensors. In Progress in Structural Engineering and Materials, Vol. 2 Issue 3, 351–358. John Wiley & Sons, Ltd. 16. D. Inaudi, S. Vurpillot and S. Lloret. 1996. In -line coherence multiplexing of displacement sensors: a fiber optic extensometer. Smart Structures and materials, SPIE Vol. 2718, 251–257. 17. M.R. Brininstool. 1987. Measuring longitudinal strain in optical fibers. Optical Engineering, Vol.26, 1112–1119. |