| □林正紋/逢甲大學土木工程學系 助理教授 □陳弘仁/逢甲大學土木水利工程學系研究所 博士 □林正原/逢甲大學土地管理學系碩士在職專班 碩士生 |
|
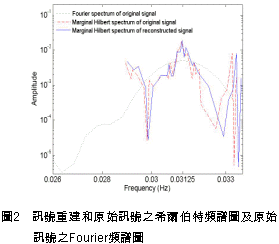
一、前言 近年來因為經驗模態分解(Empirical Mode Decomposition ,簡稱EMD)法的發明,並與希爾伯特轉換結合成希爾伯特-黃轉換(Hilbert-Huang Transform,簡稱HHT)[1,2],由於這樣的結合使得HHT有機會改變吾人對於非穩態系統的認知,並且成為描述非穩態現象的一個重要分析方法。在地震工程中,當結構系統承受任意的外部激發力時,非常依賴加速度數據的量測值,作為衡量結構系統反應狀態之依據。當加速度的數據中含有破壞的訊息時,則該資料能夠運用在結構物的破壞偵測上[3,4]。根據經驗模態分解法與希爾伯特轉換對於量測記錄之數據的分析,HHT能夠區分出結構模態與量測誤差,並且進一步偵測出系統的自然頻率與阻尼比。一般的回復力分析法通常是將空間與時間兩個自變數,藉由一系列偏微分方程式模式化,再轉換成一組常微分方程式[5],而HHT由於具有自適應性的特質,因此與傳統的回復力分析法有所不同。 尤其在頻譜圖分析中[1],HHT對於頻率具有高解析度且能量集中,而傳統的快速傅立葉轉換(Fast Fourier Transform,簡稱FFT)只能提供較少的解析度並且時常產生能量溢出現象,因此兩相比較,HHT使得FFT的功能顯得遜色許多。一般以頻率域為主的分析方法,只有當結構物維持在線性狀態時才能保持他們的有效性。然而,藉由進行等效的非時變線性系統的移動視窗分析,則像FFT[6]與小波轉換(wavelet transform)[7]等方法仍然能夠運用於非線性分析中。然而這些方法只適用於線性與微弱非線性結構物,但是對於複雜非線性的辨識問題[8]則不會成功的。因此,本文使用希爾伯特-黃轉換的方法提出一項加強噪音濾波技術,將其應用在結構物承受一維地震力作用下之結構系統識別。 二、「希爾伯特-黃轉換」之介紹 「希爾伯特-黃轉換」(Hilbert-Huang Transform,簡稱HHT)方法由於具有隨著分析訊號而調整基本性質的適應性之特點,所以在分析非線性和非穩態的訊號時,是一套非常優秀的演算法。同樣地,該法在處理線性和穩態的訊號時,也能對於分析結果提供更好的準確性。對於一個任意的時間函數x(t)而言,其希爾伯特轉換式如式(1)所示: 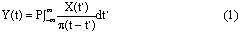 式(1)為x(t)與 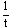 的摺積(Convolution),所以希爾伯特轉換因此能夠辨識x(t)的局部特性。 的摺積(Convolution),所以希爾伯特轉換因此能夠辨識x(t)的局部特性。將x(t)與Y(t)結合,得到可解析的訊號Z(t)如式(2):  其中 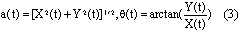 此處a(t)表訊號x(t)的瞬時振幅(Instantaneous Amplitude)、 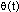 表訊號x(t)的瞬時相角(Instantaneous Phase)。而訊號x(t)的瞬時頻率 表訊號x(t)的瞬時相角(Instantaneous Phase)。而訊號x(t)的瞬時頻率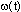 (Instantaneous Frequency)如式 (4)所示: (Instantaneous Frequency)如式 (4)所示: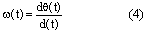 訊號x(t)的經驗模態分解(Empirical Mode Decomposition)的表示式[1]:  此處 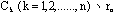 分別表訊號x(t)的本質模態函數(Intrinsic Mode Function)及殘差。而「希爾伯特-黃轉換」法是由經驗模態分解法加希爾伯特轉換組合而成的,因此根據式(1)、式(2)與式(4),可將式(5)表成下式[1]: 分別表訊號x(t)的本質模態函數(Intrinsic Mode Function)及殘差。而「希爾伯特-黃轉換」法是由經驗模態分解法加希爾伯特轉換組合而成的,因此根據式(1)、式(2)與式(4),可將式(5)表成下式[1]: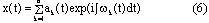 式(6)可以畫出訊號x(t)在瞬時振幅、頻率和時間的三維圖形或等高線圖,該圖形稱之為希爾伯特頻譜圖(Hilbert Spectrum, 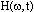 )。 )。三、加強式噪音濾波法及篩選原則 原始訊號經由經驗模態分解法處理後,可藉由挑選本質模態函數(IMFs)來重建訊號之方式,達到訊號的濾波功能。本文所提出的濾波技術,係使用式(7)[1]計算原始訊號與所有的本質模態函數之間的正交性係數,並做為挑選本質模態函數的準則。 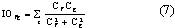 此處 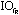 表兩個訊號間的正交性係數值, 表兩個訊號間的正交性係數值,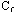 、 、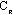 表包含訊號與該訊號的本質模態函數中任意兩個訊號。 表包含訊號與該訊號的本質模態函數中任意兩個訊號。本文對於本質模態函數之篩選準則,是藉由選擇與原始訊號正交性係數值較大的本質模態函數的挑選方式。此方式所決定的每一個本質模態函數是一個近似正交基底且具有適應性的函數;因此,這些被挑選出來的本質模態函數可能具有非線性模型的形式。而這些模型的形式是典型的低階泰勒級數展開式[9]。 四、非線性訊號的模擬 在本章節中,使用式(8)產生0∼512秒的非線性訊號[1],並將其分析結果做為隨機模型或是估算系統之自然頻率的依據。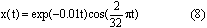 此處使用NASA授權的軟體(Hilbert Huang Transformation Data Processing System)進行訊號的分析,所以此模擬訊號的希爾伯特頻譜圖如圖1所示,顯示訊號的主要頻率大約在0.03Hz左右。 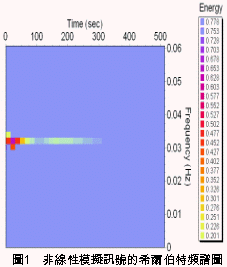 此訊號藉由經驗模態分解法可得到第一次分解,為了從這些本質模態函數中挑選出一個訊號或是訊號的第一個模態,因此使用相關性係數或是正交性係數做為挑選之依據,如表1所示。 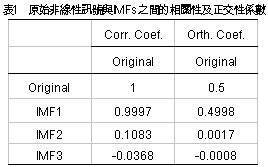 分析結果顯示相關性係數與正交性係數所挑選出的本質模態函數均為IMF1,數值分別為0.9997(最大值為1)與0.4998(最大值為0.5),對於原始的非線性訊號是最具有關聯的模態函數。 因為是藉由挑選本質模態函數來重建訊號,而此項訊號挑選程序對於獲得訊號的真實頻率(由式(8)得出頻率值為0.03125Hz)的效果,可由圖2之希爾伯特頻譜圖觀察得知。
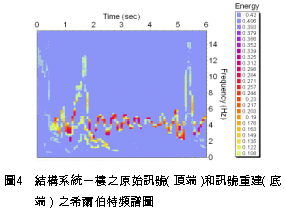
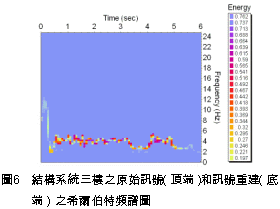
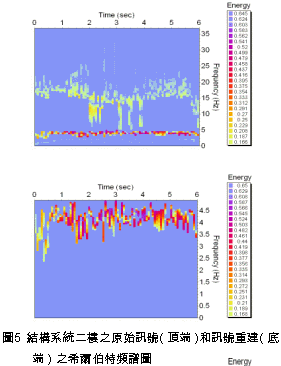
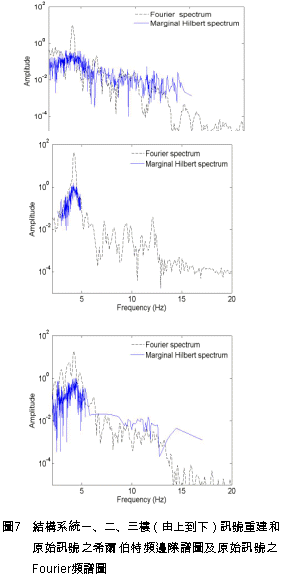
藉由挑選量測訊號的本質模態函數中,正交性係數值最大的編號作為訊號的第一模態,如表2所示,每一層樓皆挑選出IMF2。 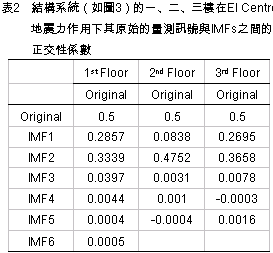 一旦挑選出IMF2做為原始訊號的重建訊號,當在此種僅使用單一的本質模態函數作為訊號的重建之條件下,該本質模態函數對於原始訊號的貢獻度是值得探討的。 圖4∼圖6的頂端各自代表結構系統1、2、3樓之原始量測訊號的希爾伯特頻譜圖,而在圖編號的底部,則是三個樓層各自挑選IMF2重建訊號後的希爾伯特頻譜圖,而在這些圖中可以觀察到結構系統的主要頻率均位於4Hz左右。 很明顯的,經由圖4∼圖6的比較,本文所提出的濾波技術已經濾掉大部份地噪音或是量測誤差,特別是在二樓,此種濾波效果更為明顯。 推究此種現象的原因有二,其一為構架中的一樓直接與振動台連接,故受其產生的非線性干擾而影響到訊號之量測;其二為三樓之激發力不足,使得一些噪音支配了量測訊號。因此,二樓有最小的噪音/訊號之比值,而該比值反應在表2中,顯示出在三個樓層的IMF2中,二樓的正交性係數值為最大。
透過加強式噪音濾波處理訊號,對於估算結構系統的自然頻率與指出破壞程度的準確性,是有可能提高評估結果的精確度。本文所提出之濾波方法不僅為尋找結構物的非線性性質方面提供了一個指引的方法,且當本質模態函數是以實測為依據的訊號所組成時,本法的準確性和效率更是不用如文獻中須依靠非線性結構系統發展出的最佳化非線性模型。因此,當在分析結構系統的非線性狀態時,移除了對於模型形式依賴的限制性後,則該法與傳統的分析方法如Fokker-Planck法及擾動法[10]有顯著的不同。
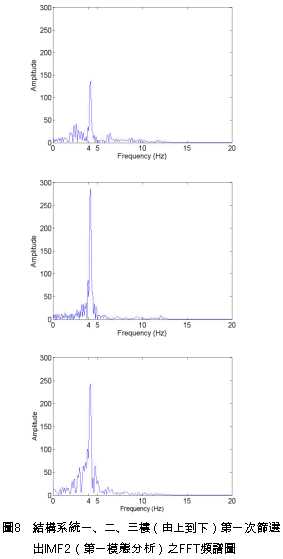
在此為了確認所挑選出來的IMF2對於實驗所用之結構系統而言,只含有一個自然頻率且相當於系統的第一個模態,故對每一層樓的IMF2進行FFT分析,如圖8所示。這些圖很清楚地顯現出只有一個最大振幅,而該振幅對應之頻率在4Hz左右。 因為本文實驗所用之結構系統含有三個模態頻率,所以有必要挑選下一個本質模態函數。從表2可以得知,由於每一樓層的IMF1之正交性係數值俱為次高,所以,挑選IMF1來估算其它模態的頻率。此處值得注意的地方,因為IMF1相當於包含訊號最高的頻率範圍,所以沒有其他
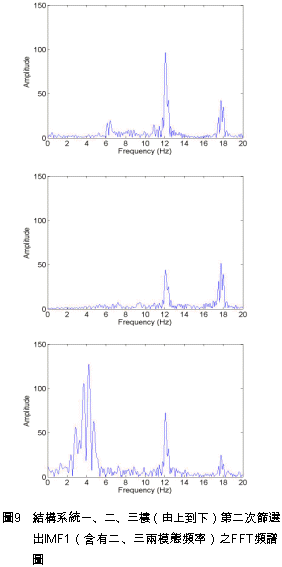
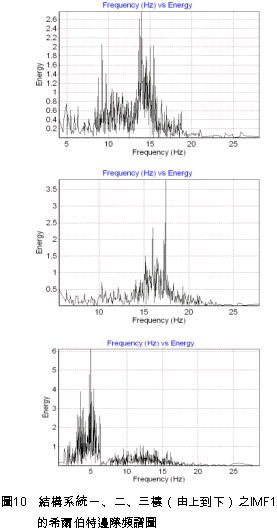
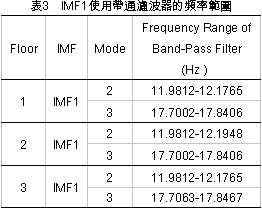
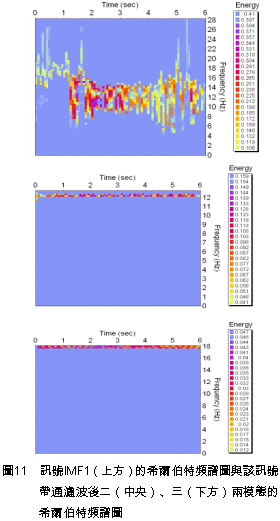
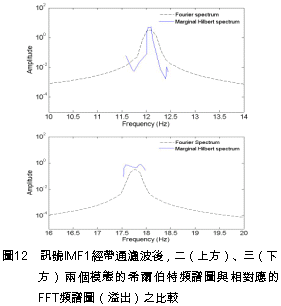
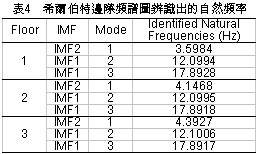
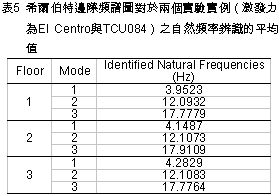
正因為所挑選的IMF1含有兩個模態,以至於無法如同IMF2在辨識第一模態頻率時,希爾伯特邊際頻譜圖能夠有效地辨識出相對應的自然頻率。 事實上,比較圖9與圖10可以得知,由於IMF1受模態混合的影響,導致其希爾伯特邊際頻譜圖(圖10)之能量最大值的頻率(一、二、三樓依序為13.689Hz、17.442Hz、4.912Hz),在某種程度上都有朝相對應之FFT圖形中振幅最大的頻率(12.1Hz、17.9Hz、4.1Hz)靠近的趨勢。 為了利用希爾伯特邊際頻譜圖在頻率上的高解析能力,因此對於含有一個以上系統模態的本質模態函數,採用帶通濾波器進行模態頻率的分析。表3列出IMF1使用帶通濾波器時,每一個模態所需的頻率範圍係使用在傅立葉頻譜圖分析中,以最大振幅值的70%[11]所對應的頻率作為截止頻率。 以一樓為例,IMF1透過帶通濾波器的處理後,其二、三兩個模態被有效地被分離出來,如圖11的希爾伯特頻譜圖所示。而該樓之二、三兩個模態在帶通濾波後,相對應的希爾伯特邊際頻譜圖如圖12所示。 此三層縮尺結構系統在以El Centro為激發力的實驗案例中,對每一層樓應用希爾伯特邊際頻譜圖所辦識的三個模態頻率如表4所示。另外,將該表連同另一個實驗案例的辨識結果(以集集大地震作為激發力),兩者之模態頻率的平均值顯示於表5。
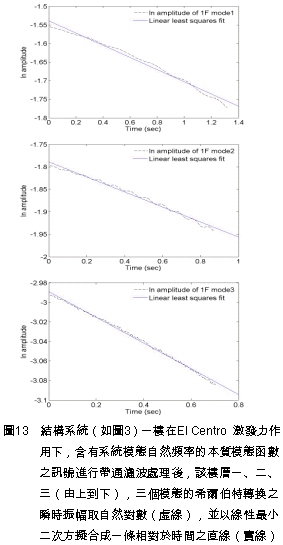
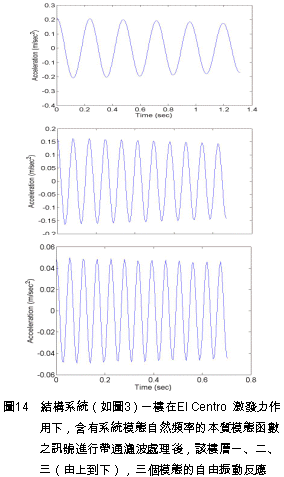
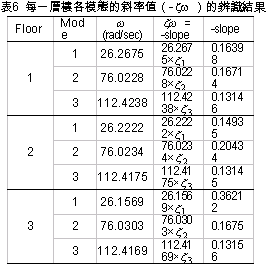
六、透過加強式噪音濾波計算阻尼比 在自由振動的模態分析[4]中,將自然頻率的辨識結果帶入式(9)與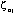 相乘,則由該式可以計算出結構系統的阻尼比。 相乘,則由該式可以計算出結構系統的阻尼比。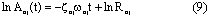 此處,n表第n個樓層、j表第j個模態、 表希爾伯特轉換所得到的瞬時振幅、 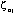 表阻尼比、 表阻尼比、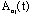 表自然頻率、R表常數。 表自然頻率、R表常數。為了計算式(9)中的 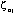 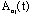 ,首先對於先前以正交性係數所篩選出含有系統模態自然頻率的本質模態函數之訊號進行帶通濾波處理步驟,並由希爾伯特邊際頻譜圖求出相對應的模態自然頻率 ,首先對於先前以正交性係數所篩選出含有系統模態自然頻率的本質模態函數之訊號進行帶通濾波處理步驟,並由希爾伯特邊際頻譜圖求出相對應的模態自然頻率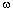 。接著對樓層各模態的瞬時振幅取自然對數(此處以以一樓承受El Centro激發力為例),則可得到如圖13虛線部分所示,並以線性最小二次方擬合成一條相對於時間之直線,如圖13實線所示,則- 。接著對樓層各模態的瞬時振幅取自然對數(此處以以一樓承受El Centro激發力為例),則可得到如圖13虛線部分所示,並以線性最小二次方擬合成一條相對於時間之直線,如圖13實線所示,則-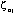 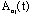 相當於該直線的斜率。 相當於該直線的斜率。為了能夠準確地找出阻尼比,此處僅僅取各模態訊號的一段短週期之歷時反應進行分析,而該歷時反應相當於模態訊號反應衰減之部分,如圖14所示。因此,可以藉由產生自由振動模態反應的方式完成模態參數的估算。
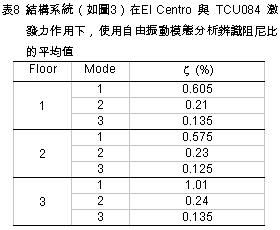
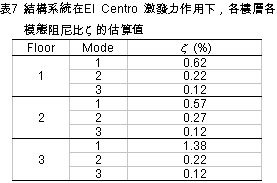
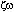 )的辨識結果如表6所示,而各樓層各振態阻尼比 )的辨識結果如表6所示,而各樓層各振態阻尼比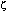 的估算值如表7所示。 的估算值如表7所示。
七、結論 在實際的工程應用上,常會遭遇許多的狀況(例如來自於量測的誤差而導致的噪音污染)使得回饋辨識系統產生模型的不確定性及量測的不確定性。同樣地,如果結構物有損傷時,為了有效地從訊號中將噪音分離出來,則以HHT為基礎的辨識技術可被運用在處理時變(Time-Varying)結構系統的破壞偵測上。因此,本章在估算與時間相關之結構物的特性(如模態自然頻率)時以下列步驟進行: (1) 使用EMD重建訊號並使用正交性係數做為篩選的準則。 (2) 由帶通濾波器分離出模態訊號。 (3) 藉由希爾伯特邊際頻譜圖決定出系統各模態的自然頻率。 所以本章節所提出的方法,包含下列優點: (1) 原始的加速度訊號必須先執行EMD,以避免該訊號受到嚴重的噪音污染。 (2) 正交性係數提供了挑選本質模態函數(IMFs)的能力。 (3) 本文所提出之濾波方法不僅為尋找結構物的非線性性質方面提供了一個指引的方法,因為本質模態函數是以實測為依據的訊號所組成,本法的準確性和效率更是不用如文獻中須依靠非線性結構系統發展出的最佳化非線性模型。 八、誌謝 非常感謝行政院國家科學委員會贊助 (research grant NSC 96-2221-E-035-038)此篇研究論文。■參考文獻 1. Huang, N.E., Shen, Z., Long, S.R., Wu, M.C., Shih, H.H., Zheng, Q., Yen, N.C., Tung, C. C., Liu, H.H., 1998, “The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis,” Procedures of the Royal Society of London, 454, pp. 903-995.2. Huang, N.E., Wu, M.C., Long, S.R., Shen, S.P., Qu, W., Gloersen, P., Fan, K.L., 2003, “A confidence limit for the empirical mode decomposition and Hilbert spectral analysis,” Procedures of the Royal Society of London, 459, pp. 2317-2345. 3. Yang, J.N., Lin, S., Pan, S., 2002, “Damage identification of structures using Hilbert-Huang spectral analysis,” ASCE 15th Engineering Mechanics Conference, Columbia University, New York. 4. Yang, J.N., Lei, Y., Lin, S., Huang, N., 2004, “Hilbert-Huang based approach for structural damage detection,” Journal of Engineering Mechanics, 130(1), pp. 85-95. 5. Wen, Y.K., 1989, “Methods of random vibration for inelastic structures,” Applied Mechanics Review, 42(2), pp. 39-52. 6. McVerry, G.H., 1980, “Structural identification in the frequency domain from earthquake records,” Earthquake Engineering and Structural Dynamics, 8, pp. 161-180. 7. Kitada, Y., 1998, “Identification of nonlinear structural dynamic systems using wavelets,” Journal of Engineering Mechanics, 124(10), pp. 1059-1066. 8. Koh, C.G., See, L.M., 1994, “Identification and uncertainty estimation of structural parameters,” Journal of Engineering Mechanics, 120(6), pp. 1219-1236. 9. Stry, G.I., Mook, D.J., 1991, “Correlation techniques in robust nonlinear system realization / identification,” Advances in the Astronautical Sciences: Proceedings of the AAS/AIAA Spaceflight Mechanics Meetings, 75(1), pp. 453-469. 10. Atalik, T.S., Utku, S., 1976, “Stochastic linearization of multi-degree-of-freedom non-linear systems,” Earthquake Engineering and Structural Dynamics, 4, pp. 411-420. 11. Etter, D.M., 1993, Engineering Problem Solving with Matlab, Prentice-Hall. 本篇為譯文,翻譯自 Lin, J.-W., Huang, C.-W. (2009). “Hilbert-Huang Transform Based Noise Filtering for the Identification of Structural Systems,” Journal of Civil Engineering and Architecture, Vol.3, No.3, pp.1-10. |