| □林楚儒／亞新工程顧問公司 正工程師 |
|
一、前言 為表現結構上的力與美，就屬摩天大樓及大跨徑之橋梁，為了支撐起如此大跨徑之混凝土橋梁，預力的理論便成為其後勤之支援了！本文將詳細介紹預力計算的原理，預力之施拉將產生以下之現象：1.預力摩擦損耗 2.端錨要錨碇於錨座時的預力滑動損耗 3.大梁彈性縮短時所引起之預力損耗 4.混凝土的潛變與乾縮所造成之預力損耗 5.對大梁產生等似預力系統 6.預力鋼腱之縮短量 7.拋物線以外之鋼腱曲線。二、預力摩擦損耗 詳參考文獻[1]，本文就不再贅述。三、端錨要錨碇於錨座時的預力滑動損耗 錨碇座之預力滑動的現象：錨碇座之鎖片係像木楔一樣，在內壁要如圖2所示車成螺紋，並切成兩半或3片，與鋼腱一起插入如圖1之傾斜孔道內，鋼腱係用油壓千斤頂拉長，並於錨碇座頂住，之後千斤頂鬆弛，將所施拉之力移傳給錨碇座，同時公螺紋表現出如鯊魚牙齒一樣，把鋼絞線緊緊咬住，並以一個衝力將之拉入錨碇座的斜孔道內，穩穩地卡住在錨碇座鈑及鎖片楔之間，於釋放油壓千斤頂時，將所施拉力傳給大梁後，便會使鋼腱有所滑動，使所插入的鋼絞線之預力造成損耗，所謂錨碇滑動的術語，其實就是鎖片楔跟鋼腱一起滑動而已，但一般皆簡單地稱為錨碇的滑動，滑動對預力最大的影響處位於錨碇座最外端，但可藉鋼腱跟套管之間的摩擦力沿著套管長度止住，至某個長度滑動所造成的預力損耗便會為零，此長度謂之為影響長度，由於一端的滑動造成預力損耗的現象，詳參考文獻[1]，本文就不再贅述。   四、先拉法的預力大梁之預力分佈情形 圖3顯示預鑄大梁的簡易先拉法系統，與傳統的後拉法的預力系統不同，將於以下討論之，表1 顯現先拉法與後拉法的各自優點，而表2卻顯現兩系統的各自缺點：圖4表現出先拉法的預力大梁在其兩端須有發展長度(developing length)之缺點，因此靠兩端之附近不能如後拉法可期待能抵抗強大外力荷重，與後拉法的預力鋼腱不同的是：預力係靠施拉端且藉千斤頂將拉力移轉到端部或從被施拉端傳遞過來，大梁兩端都受到推力，但因套管內摩擦關係，由兩端向中央的預力逐漸降低，摩擦力並不永遠都是缺點，如對摩托車的輪胎而言，摩擦力幫助車子行駛時之穩定，以免小轉彎即傾倒，在後拉法預力大梁內，摩擦力幫助將小部份預力傳給混凝土梁；對先拉法預力大梁而言，在澆灌混凝土前，先施拉預力，就不需錨碇系統及套管，澆置混凝土後以蒸汽養護1至2天，好讓混凝土產生80%以上強度，以便鋼腱如圖3可被混凝土的黏著力所充分裹握住，鋼腱在梁兩端可用鋸片切掉，兩端壓力突然藉由鋼腱與混凝土之間的黏著力傳給混凝土梁，而因端點在割除端部鋼腱後，已無支承或端錨可接受力量， 此時大梁的兩端點之預力為零，因此發展長度L 是需要的，以便產生足夠之強度以接收從施拉設備所傳來之壓力，在發展長度未產生前不能有過大之外力施加於大梁上，也是可理解的。 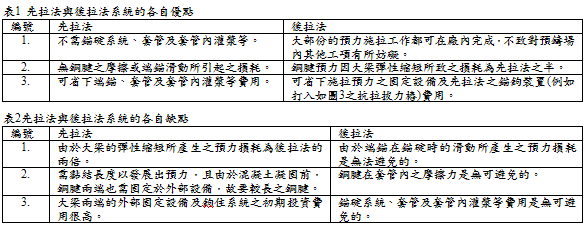 五、預力由於混凝土之潛變乾縮所產生之損耗 六、建立預力的等似荷重系統 以上兩節詳參考文獻[1]，本文就不再贅敘。七、大梁兩端在施預力時之鋼腱伸長量 (一)引言鋼腱伸長量做為鋼腱是否施拉到達設計預力值的量測數據之重要指標，如果沒有套管內的預力摩擦力之干擾，通常油壓磅表來量測鋼腱是否達到所需預力值是足夠正確的。伸長量又是鋼腱在套管內是否碰到困難的指標，例如套管不尋常地變形或某處有過大之粗糙度，若有此種情形，預力將降至設計值之下，於是伸長量便小於預定值，而油壓磅表所顯現施拉預力已到達設計值，但繼續施拉以得到預定伸長量，則會使鋼腱在油壓千斤頂或錨碇鎖片楔處斷裂，此情況下，建議解除油壓力而將鋼腱抽出才是上策，鋼腱左右抽動幾次，以磨平套管內的粗糙物，將水洗式的油塗抹於鋼腱上做為潤滑劑，再次施拉預力，如果伸長量並未顯示出有拉預力之困境的訊號，就表示與計算值相差在5%的誤差以內，於是在錨碇鋼腱以後，潤滑油脂可用水沖洗掉，再以空氣壓縮機吹進套管內使鋼腱或套管乾燥後，準備灌水泥漿，要注意水泥需用細篩子篩除結塊之水泥粉顆粒，以免長套管灌漿時，受阻礙而灌不進去。 (二)鋼腱伸長量之計算 鋼腱伸長量  可以很容易以 的公式來定義，此處 為鋼腱內之應力，對很短之鋼腱，其長度介於10~45 m 之間，最好採取單邊施拉預力，不必考慮微不足道的另一邊之預力的摩擦損耗，係為了節省勞力而已，因為此邊預力受到端錨的滑動損失，兩相比起來，實差不了多少，又更短之鋼腱採雙邊施拉預力時，滑動損失後之預力被強迫在中央處止住，僅管如此，計算鋼腱伸長量時，並不考慮端錨的滑動損失，因伸長量的發生係在油壓力移轉給錨碇裝置前。值得注意的是：30多年前雙邊施拉需要兩組工人及兩組油壓設備，使左邊之伸長量A等於右邊之B。理論上A及B須如圖6所示完全相同，但這很難達成，且如圖7所示並非必要，因為無法控制兩端的工人精確地拉出相同之長度，不過對特定的鋼腱之兩端合起來之伸長量C是一個常數，使C=A+B。因為我們無法保證A永遠等於B，那為什麼要浪費兩組工人及兩組油壓設備呢？我們不如僅用一組人力及機具，先一邊施拉後再施拉另一邊，也一樣達成雙邊施拉預力的目標如圖8所示。施工計畫中須含施拉預力之伸長量的詳細計算，以下之章節裏將說明兩端施拉預力之伸長量計算的範例，圖9顯示一錨碇座如何插入鎖片楔子以夾住鋼絞線，此鎖片楔子要用鎚子輕輕地將之做初步壓緊，以便另一端可開始試著施拉預力，初始施拉係嘗試確定兩端之楔子是否能將鋼腱固定住，之後再將施拉之油壓鬆掉，於是完整的及實際預力之施拉便可正式開始。    茲介紹以下之計算例以顯示施拉方式不同的伸長量值。已知一鋼腱長度為40 m，表3僅為左邊施拉；表4僅為右邊施拉；表5為同時兩邊施拉；表6為先左邊施拉，然後再施拉右邊之鋼腱。 由於在左邊施拉的鋼腱之左邊伸長量為：   由於在右邊施拉的鋼腱之右邊伸長量也一樣為： =243.8 mm兩邊同時施拉的鋼腱之左右邊各伸長量為：   =13.18cm =131.8 mm 左邊右邊皆相同。左邊施拉的鋼腱之左邊伸長量為： 參考前述之計算，我們得到 左邊伸長量 =243.8 mm，於是之後轉為施拉右邊的鋼腱之右邊伸長量為： = 1.99 cm = 19.9 mm─於右端。請注意 (243.8+19.9)/2 = 131.85 mm 與表5所計算的幾乎相同。     八、三次方曲線之鋼腱方程式 (一)引言我們所熟悉的預力混凝土梁之鋼腱的曲線為二次拋物線，但在歐洲，尤其是德國或奧地利，人們採用新思維而將上述之拋物線方程式拋棄掉，以選擇比較和緩之3次方函數的曲鋼腱，一些橋梁軟體如RM[4] 採用3次方函數，反而拋物線變化的資料卻無法輸入程式裏，因此鼓勵大家採取新的考量，所以不流行之拋物線變化的曲鋼腱想法，應予以拋棄掉，而採用革命性的3次曲線，其數學公式將在下面章節裏首先詳細介紹後，再比較兩者之優缺點。 (二) 3次方曲線的數學公式之導引 如圖10所示，通過點A及B之拋物線和直線各自被稱為a和b，它們在點B之斜率為  和 。點B之拋物線的斜率為直線之兩倍，如果可採用直線的話，通過兩點之斜率，不就可降低嗎？事實上，當要轉彎鋼腱時，曲線是必須的，而在B點的斜率採取中庸之道，如此甚好，因3次方曲線之斜率係介於直線跟拋物線之間。3次方曲線之通式為  ，且斜率為 .在A點之邊界條件：  而在B點：  由於採用直線跟拋物線的斜率之平均值，1.5的係數被公認最中庸及最適當的，因此點A之D=0，C=0。 且  ，為了要求出這些係數，便得到 3次方函數及其導數就成為  。於是其曲率函數很清楚地為 (三)三次曲線跟拋物線的比較 從以上對曲線函數的導引，我們就可體會到三次曲線的斜率是何等和緩地改變，以一樣的長度之鋼腱而言，比起拋物線，因斜率變化較平緩，所以有較少的摩擦損耗，但缺點是三次曲線的預力較難計算，而且在支承點附近也比較不能提供充足的垂直分量之剪力抵抗強度。 (四)三次曲線之鋼腱的等似荷重 基本上曲鋼腱都會有垂直等似荷重，在不考慮預力損耗下之垂直等似荷重，係如圖11所示，但考慮預力損耗時之垂直等似荷重係如圖12~15所示。 對垂直方向的平衡而言：  解出第一象限：  解出第二象限：  解出第三象限：  最後解出第四象限：  軸向等似荷重  每一桿件段於節點B之彎矩等似荷重為M，於是  對節點A取彎矩，我們得到：  , 於是  上述之軸向、垂直之等似荷重，以及點彎矩皆可輸入任何結構軟體，以求出桿件內預力所引起之反應力。 點彎矩可以在桿件兩端點之力偶(couple of forces)來取代，然後與下一個桿件組合起來以求出平順之彎矩反應力，值得注意的是要進行結構分析時，須考慮在3度空間構架之桿件的結合情形，我們也要把等似荷重移轉到全域座標系統(global coordinate system)，才能得到正確之反應力及撓曲量。     僅憑徒手，當然很難繪出三次曲線，本文免費贈送以下之AutoCad lisp： (defun lines (ptset)(mapcar 'command (cons "line" ptset))(command "")) (defun line (pts pte) (command "line" pts pte "")) (defun c:cubi(/ v vz h ct ce n dx dzz dyy dxx sx pt i x y z lines) 以上的程式語言是AutoCad 專用的Auto lisp 名字叫做cubi.lsp，讀者只要用微軟office的筆記本(Notepad)工具鍵入便可存檔，然後再載入─“ (load”cubi”) ”進AutoCad環境內，打出cubi的指令，且依螢幕的訊息指示，用滑鼠點曲線的兩個點就可繪出平滑之三次曲線。 (六)結語 三次曲線之鋼腱目前很少見，但這是一個革命性的改變，可促進鋼腱材料的效率，為地球的節能減炭，盡一番心力。 九、結論 以上所談及之等似荷重都只參考到桿件的局部座標而已，讀者須利用高等結構學上教科書之方向旋轉矩陣(rotation matrix)，轉成全域座標系統，有些商業程式對兩端施拉預力之鋼腱伸長量僅有總伸長量而已，並未載明先左邊施拉時，左邊伸長多少?再移到右邊施拉後，右邊伸長又是多少?以便與油壓千斤頂的磅錶讀數互相校核。應鼓勵施拉鋼腱時，設計上之左右端的伸長量能明明白白地被標示出來。參考文獻 1.林楚儒─節塊施工的連續預力梁之分析與設計, 文笙書局股份有限公司民國84年02月2.The C Range Post-tensioning System, Freyssinet International, 1 Bis, Rue du Petit-Clamart-Bat. C 78140 Velizy-Villacoublay, France. 3.VSL International Ltd. Bernstrasse 9, Lyssach-CH 3421, Switerland. 4.RM-SPACEFRAME, TDV-Technische Datenver-arbeitung, gesellschaft m.b.h. Heinz Pircher und partner, A-8010 Graz-Luthergasse 4. |
